Unit 10: Projectile and Satellite Motion
The curved flight of a golf ball appears different from the continuous rotation of a satellite around Earth. After completing this unit, you should be able to explain how both movements are forms of projectile motion.
Learning Outcomes
By the end of this unit, you should be able to
- give examples of projectiles launched horizontally or at different angles.
- explain how a fast-moving projectile can become a satellite.
- discuss the difference between circular and elliptical satellite orbits.
- state Kepler’s laws of planetary motion.
- discuss conservation of energy in satellite and planetary motion.
- define escape speed and explain its relation to potential energy.
eText Material
Reading Assignment
Read the following sections in Chapter 10 of the eText:
- 10.1: Projectile Motion
- 10.2: Fast-Moving Projectiles—Satellites
- 10.3: Circular Satellite Orbits
- 10.4: Elliptical Orbits
- 10.5: Kepler’s Laws of Planetary Motion
- 10.6: Energy Conservation and Satellite Motion
- 10.7: Escape Speed
Supplementary learning resources are available on the Mastering Physics learning platform.
Additional Reading
Projectile Motion
You might expect the analysis of motion along a curved path to be more complicated than that of motion along a straight line (discussed in Unit 3). However, projectile motion can be analyzed simply and elegantly using your existing knowledge of the kinematics of linear motion and vector addition.
To analyze projectile motion, you first resolve the initial velocity into two components: along the horizontal direction and along the vertical direction. Then you analyze the motion in both directions independently. Since the acceleration due to gravity is vertical (directed downward), it affects only the vertical component of the velocity. The horizontal component is not affected by gravity, so it stays constant during the entire motion.
In a real-life situation, both the horizontal and the vertical velocities are affected by air resistance. However, to make your work as simple as possible, you will consider an ideal atmosphere in which there is no air drag or wind turbulence to complicate the calculations. (You can be sure, however, that when NASA sends a rocket into space, they do take into consideration air resistance, wind velocity, variations in the acceleration due to gravity, and a host of other variables. Your task here is much simpler!)
Figure 10.1: An object in projectile motion.
Consider an object projected from ground with an initial velocity $v_i$ and at an angle $\theta_i$ above the horizontal (see Figure 10.1). To analyze the motion, you resolve the object’s velocity into horizontal ($v_x$) and vertical ($v_y$) components. Due to the absence of horizontal forces, $v_x$ remains constant during the entire flight of the projectile. The upward vertical velocity, however, decreases in value as time passes due to the downward gravitational force. As a result, the velocity vector gradually tilts toward the $x$ axis, becoming perfectly horizontal (i.e., $v_y = 0$) when the projectile reaches its maximum height.
From that point on, $v_y$ becomes negative and starts to increase in magnitude. The resultant velocity tilts below the horizontal direction, and the projectile continues to descend until it hits the ground, with a final velocity $v_f = v_i$ at $\theta_f = \theta_i$, as shown in Figure 10.1. Also, note that the time it takes the projectile to rise to its maximum height is equal to the time it takes to fall back to the ground.
Video 4.1: Projectile motion.
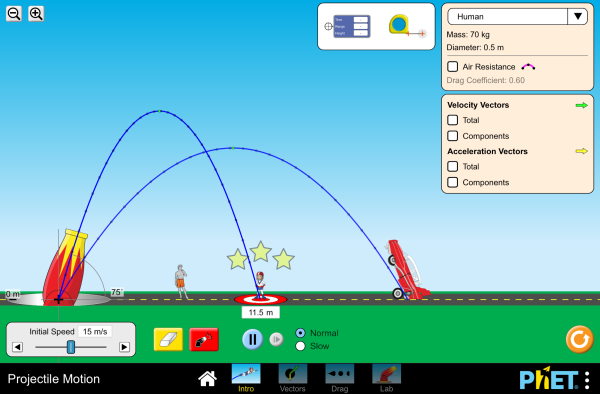
Simulation
Run the Projectile Motion simulation to learn about projectile motion by launching various objects.
Simulation by PhET Interactive Simulations, University of Colorado Boulder, licensed under CC-BY-4.0 (https://phet.colorado.edu)
Satellites
To help you understand the orbital motions of satellites, here is a fictitious example. A soldier is stationed at the top of a high cliff overlooking the ocean to test a powerful new piece of artillery that has adjustable projectile velocity. The soldier directs the barrel in the horizontal direction and fires shells out over the ocean. The tests begin with a relatively small firing speed, which is gradually increased.
When the firing range is small relative to the size of Earth, the vertical distance traveled by two shells fired horizontally at different speeds is essentially constant, as shown in Figure 10.2(a). However, as the firing speed increases, an expert evaluating the tests must take into consideration the curvature of Earth, as shown in Figure 10.2(b).
Figure 10.2: Motion of an artillery shell shot horizontally at different initial speeds.
If the soldier keeps increasing the projectile velocity, the shell will travel a relatively large distance around the globe before it reaches sea level. If the shell is given sufficient initial velocity, it will remain at the same altitude above the ocean while travelling in a perfect circle around Earth. In such a case, the soldier will have actually placed a satellite into orbit that (neglecting air resistance) will continue to rotate around the planet, as shown in Figure 10.2(c). The soldier will have to change locations; otherwise, once the shell makes a full rotation around Earth, it will strike the expensive artillery!
Consider a satellite (mass $m$) in orbit around Earth (mass $M_\text{E}$). The satellite rotates at a uniform speed $v$ along a circular path of radius $r$ around the planet. In this case, the force of gravity ($F_g$) exerted by Earth on the satellite provides the required centripetal force ($F_c$), such that
\begin{align} F_c &= F_g \nonumber\\[6pt] \Rightarrow\quad \frac{m v^2}{r} &= G\, \frac{m M_\text{E}}{r^2} \nonumber\\[6pt] \Rightarrow\quad v^2 &= \frac{G M_\text{E}}{r} \end{align}
So the speed of the satellite depends on the radius of rotation, according to the equation
\begin{equation} v = \sqrt{\frac{G M_\text{E}}{r}} \label{unit10_vGMEr} \end{equation}
Video 10.1: Three satellites placed at different orbits around Earth.
Equation 10.2 suggests that satellites placed at higher orbits move slower than satellites at lower altitudes (see Video 10.1). The period of rotation ($T$) of the satellite also depends on the radius of rotation, where
\begin{align} T &= \frac{2 \pi\, r}{v} \nonumber\\[6pt] &= 2\pi\, r\, \sqrt{\frac{r}{G M_\text{E}}} \nonumber\\[6pt] &= \frac{2\pi\, r^{3/2}}{\sqrt{G M_\text{E}}} \label{unit13_Ta} \end{align}
By squaring both sides, you can express Equation 10.3 as \begin{equation} T^2 = \left(\frac{4\pi^2}{G M_\text{E}}\right) r^3 \label{unit13_T2r3} \end{equation} which is the mathematical form of Kepler’s third law.
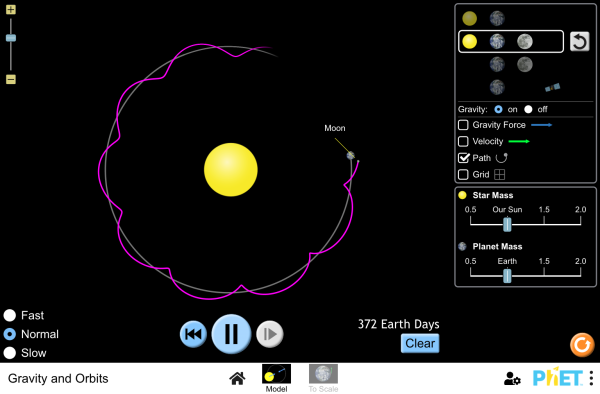
Simulation
Run the Gravity and Orbits simulation to model orbital motion.
Simulation by PhET Interactive Simulations, University of Colorado Boulder, licensed under CC-BY-4.0 (https://phet.colorado.edu)
Questions
The following questions are selected from the end of Chapter 10 of the eText. It is important to your learning that you try to answer each question independently before you read through the answer and explanation given.
For questions that ask you to explain, defend, or discuss your answer, the response revealed by the Answer button would earn you only partial marks on a quiz or exam in this course. Use the Answer to help you formulate a complete answer before you select the Explanation button to check your work.
Note that some questions have been adapted to suit the format of this course.
Chapter 10
Question 14
How much time does a satellite in close orbit about the Earth take to complete each revolution?
Answer
83 min
Explanation
To follow an orbit close to Earth, a satellite must have a tangential speed of 8 km/s. Since the circumference of Earth is about 40,000 km, the satellite would make a complete revolution in a period of \begin{align} T &= \frac{40{,}000\,\text{km}}{8\,\text{km/s}} \nonumber\\[6pt] &= 5000\,\text{s} \quad (\text{or}\; 83\,\text{min}) \end{align}
Chapter 10
Question 31
A baseball projected with an initial velocity of 141 m/s at an angle of 45° follows a parabolic path and hits a balloon at the top of its trajectory. Neglecting air resistance, show that the ball hits the balloon at a speed of 100 m/s.
Diagram
Video Q10.31
Answer
Since the baseball is projected with an initial velocity of 141 m/s at an angle of 45°, the horizontal and the vertical components each have an initial value equal to 100 m/s. Note that \begin{equation} \sqrt{(100\,\text{m/s})^2 + (100\,\text{m/s})^2} = 141\,\text{m/s} \nonumber\\[6pt] \end{equation}
In the absence of air resistance, the baseball does not experience any horizontal acceleration and its speed in this direction remains constant. The ball’s upward speed, however, decreases (due to gravity) at a rate of 10 m/s every second. During the moment when it is at maximum height, the baseball loses all its vertical speed but continues to move horizontally at 100 m/s (see Video Q10.31).
Chapter 10
Question 40
When you roll a ball off a tabletop, will the time it takes to hit the floor depend on the speed of the ball? (Will a fast ball take a longer time to hit the floor?) Defend your answer.
Answer
The time the ball is airborne does not depend on its initial horizontal speed.
Explanation
Here, the ball rolls off the tabletop in the horizontal direction and performs free fall with zero initial vertical velocity. Note that the vertical portion of the motion is what brings the ball down to the floor and, therefore, determines the time of flight (assuming air resistance is negligible). You can conclude that objects rolling off the table at different horizontal speeds will take the same time to hit the floor.
Chapter 10
Question 42
If you toss a ball vertically upward in a uniformly moving train, it returns to its starting place. Will it do the same if the train is accelerating? Explain.
Answer
No. While the ball is in the air, its horizontal speed remains constant, while the train’s speed continues to change. For example, while speeding up, the train moves ahead of the ball, which then falls behind you. The opposite happens if the train is slowing down.
Chapter 10
Question 44
Suppose you drop a care package from an airplane traveling at constant velocity, and air resistance doesn’t affect the falling package.
- What will be its falling path as observed by someone at rest on the ground off to the side where there’s a clear view?
- What will be the falling path as observed by you looking downward from the airplane?
- Where will the package strike the ground, relative to you in the airplane?
- Where will it strike in the more realistic case in which air resistance does affect the fall?
Diagram
Video Q10.44
Answer
- An observer on the ground will see the package follow a curved path as it falls, as shown in Video Q10.44.
- You (on the airplane) will see the package fall straight down relative to the airplane.
- The package will strike the ground at a point directly under the airplane at that moment.
- In a real situation, air drag will cause the package to strike the ground at a point behind the airplane at that moment.
Explanation
From the perspective of an observer on the ground, the package falls freely while maintaining a horizontal speed equal to that of the airplane. So, while falling to the ground, the package remains directly below the airplane. In this case, the package behaves like a projectile, as shown in Video Q10.44.
From your perspective in the airplane, the package falls straight down. This is because in your reference frame, the package has zero horizontal speed, while the ground appears to move horizontally backward at a speed equal to that of the airplane. Therefore, when the package strikes the ground, the airplane is directly over the point of impact.
In a real situation, however, air resistance reduces both the horizontal and the vertical speeds of a projectile. Therefore, the package strikes the ground behind the airplane.
Chapter 10
Question 47
If air drag can be neglected, at what point in its trajectory does an upwardly thrown baseball have its minimum speed? How does this compare with the horizontal component of its velocity at other points?
Hint
Note that the ball loses all its vertical velocity at the top of its trajectory, while its horizontal velocity is unaffected.
Diagram
Video Q10.47
Answer
When you throw a baseball upward, you give it an initial velocity with horizontal and vertical components. In the absence of air resistance, the horizontal component remains unchanged because no force acts on the ball in this direction. The vertical component, however, decreases as the ball rises above the ground, until the vertical velocity becomes zero at the highest point of the ball’s trajectory (see Video Q10.47). At this point, the ball slows to its minimum speed, which is equal to its constant horizontal speed ($v_x$ in Video Q10.47).
Chapter 10
Question 48
When Bullseye Bill fires a rifle at a distant target, why isn’t the barrel aligned so that it points exactly at the target?
Answer
Bullseye Bill has to aim the barrel slightly higher than the target because the bullet does not travel in a straight line. The bullet curves toward the ground during its flight.
Diagram
Figure Q10.48
Explanation
While in the air, a bullet moves as a projectile because it is pulled down by the force of gravity. Therefore, if the rifle’s barrel is pointed exactly at the target, the bullet will hit below the projected line, as shown in Figure Q10.48. To compensate for this deviation, the barrel should be slightly elevated.
Chapter 10
Question 52
Since the Moon is gravitationally attracted to Earth, why doesn’t it simply crash into Earth?
Answer
Because of its tangential speed.
Explanation
If the Moon had no rotational motion around Earth, the force of gravity would pull the Moon directly toward Earth and the two bodies would collide. If the Moon had a relatively small tangential speed, it would eventually approach and hit Earth’s surface like a projectile.
In reality, the Moon revolves around Earth in a nearly circular orbit with a radius of 384,000 km at a speed of about 1 km/s. The force of gravity provides the required centripetal force.
Chapter 10
Question 54
Which planets have a more-than-one-Earth-year period, planets nearer than Earth to the Sun or planets farther from the Sun than Earth?
Answer
Planets farther from the Sun than Earth.
Explanation
Planets farther from the Sun move slower and in larger orbits than Earth. According to Kepler’s third law, the square of the orbital period of a planet is directly proportional to the cube of its average distance from the Sun, or \begin{equation} T^2 \propto r^3 \end{equation} Thus, the period of rotation $T$ increases with the distance $r$ from the Sun. The outer planets in the solar system therefore have periods of rotation longer than one Earth year (yr):
- Mars: 1.9 yr
- Jupiter: 12 yr
- Saturn: 29 yr
- Uranus: 84 yr
- Neptune: 165 yr
Chapter 10
Question 56
Does the speed of a falling object depend on its mass? Does the speed of a satellite in orbit depend on its mass? Defend your answers.
Hint
The net force in each case is proportional to the object’s mass.
Answer
A freely falling object of mass $m$ experiences a net downward force equal to the force gravity on the object. By applying Newton’s second law to this motion, you have
\begin{align} m a &= F_g \nonumber\\[6pt] \Rightarrow\quad ma &= G\, \frac{m M_\text{E}}{R_\text{E}^2} \nonumber\\[6pt] \Rightarrow\quad a &= \frac{G M_\text{E}}{R_\text{E}^2} = g \label{u10_q56_ag} \end{align}
Equation 10.7 shows that all freely falling objects experience equal acceleration ($g$) and gain speed at the same rate, regardless of their mass.
The centripetal force ($F_c$) required for rotational motion is provided by the force of gravity ($F_g$) on the satellite. Note that both forces are proportional to the satellite’s mass ($m$), so you can write
\begin{align} F_c &= F_g \nonumber\\[6pt] \Rightarrow\quad \frac{m v^2}{r} &= G\, \frac{m M_\text{E}}{r^2} \nonumber\\[6pt] \Rightarrow\quad v^2 &= \frac{G M_\text{E}}{r} \nonumber\\[6pt] \Rightarrow\quad v &= \sqrt{\frac{G M_\text{E}}{r}}\label{u10_q56_v} \end{align}
Equation 10.8 shows that the satellite’s speed ($v$) is independent of its own mass but dependent on Earth’s mass ($M_\text{E}$).
Chapter 10
Question 62
Earth is closer to the Sun in December than in June. In which of these two months is Earth moving faster around the Sun?
Answer
December
Explanation
The total mechanical energy of the Sun–Earth system is a conserved quantity, and it is equal to the sum of Earth’s kinetic energy (KE) and gravitational potential energy (PE). In other words, $\text{KE} + \text{PE}$ is the same at any point on Earth’s orbit around the Sun. Since PE is smaller at locations closer to the Sun, KE (and therefore speed) increases at such locations.
Chapter 10
Question 65
Why is work done by the force of gravity on a satellite when it moves from one part of an elliptical orbit to another, but no work is involved when it moves from one part of a circular orbit to another?
Answer
Work is done on an object when at least part of the applied force is along the direction of motion. In a circular orbit, the force of gravity continuously acts perpendicular to the direction of motion and, therefore, no work is done on the satellite. However, in an elliptical orbit, there is always a component of the gravitational pull parallel to the satellite’s path (except at the apogee and perigee points). Therefore, work is done on the satellite in this case.
Chapter 10
Question 78
What is the maximum possible speed of impact upon the Earth’s surface for a faraway body initially at rest that falls to Earth by virtue of Earth’s gravity only?
Answer
11.2 km/s
Explanation
Escape speed is the minimum initial speed required for an object launched vertically upward to overcome the force of Earth’s gravity and not fall back to the ground. This speed is equal to 11.2 km/s.
An object launched straight up at 11.2 km/s will eventually stop at a distance far from Earth when all the object’s initial KE is converted into gravitational PE. When the object starts to fall back toward Earth, the process is reversed: PE is now converted into KE. Just before it hits Earth’s surface, the object reaches its initial KE again. Therefore, the maximum speed of impact on Earth’s surface is equal to the launch speed of 11.2 km/s (the escape speed). If launched at a greater speed, the object will not return to Earth.
Chapter 10
Question 95
In an accidental explosion, a satellite breaks in half while in circular orbit about Earth. What is the fate of the half brought momentarily to rest? Discuss what happens to the other half of the satellite.
Hint
The first half falls straight down, while the other half leaves Earth.
Answer
Based on the law of conservation of momentum, if one half of the satellite comes to rest after the explosion, the other half (of equal mass) will move away at twice the original speed. As a result, the part that freezes in orbit simply falls straight down under the influence of its weight. The remaining section has enough speed to escape its orbit about Earth and become a satellite of the Sun.
Exercises
Spend some time completing the following exercises to test your understanding of the main concepts in Chapter 10 and increase your efficiency in answering exam questions.
End-of-Chapter Practice Questions
Answer questions 3, 7, 9, 11, 13, 15, 17, 21, 33, 37, 39, 41, 49, 51, 57, 59, 63, 69, 79, 85, 89, and 91 from Chapter 10 of the eText. If you require assistance, please contact your tutor. The answers are provided at the end of the eText.
Quiz 2
Before moving on to Unit 11, complete Quiz 2, which covers Units 6–10. For more information and to take the quiz, see the Quizzes section on the course home page. This quiz is worth 10% of your course grade.