Unit 7: Energy
The thrill of a roller coaster ride, regardless of design complexity, is based on the fundamental law of conservation of energy. The large amount of potential energy stored in the cars at the top of the first hill is the only fuel that drives these cars through the rest of the trip. After completing this unit, you should be able to explain why the first hill is always the highest point of the roller coaster.
Learning Outcomes
By the end of this unit, you should be able to
- define work and power in physics and state the unit of each quantity.
- define potential energy, kinetic energy, and mechanical energy.
- state and write the mathematical representation of the work–energy theorem.
- state the law of conservation of energy and discuss its implications.
- give examples of simple machines and discuss the notion of efficiency.
- name different sources of energy used by our society and discuss the role of food as the source of energy necessary for life.
eText Material
Reading Assignment
Read the following sections in Chapter 7 of the eText:
- 7.1: Work
- 7.2: Power
- 7.3: Potential Energy
- 7.4: Kinetic Energy
- 7.5: Work–Energy Theorem
- 7.6: Conservation of Energy
- 7.7: Machines
- 7.8: Efficiency
- 7.9: Major Sources of Energy
Supplementary learning resources are available on the Mastering Physics learning platform.
Additional Reading
Energy and Work
The two main concepts in this unit are energy and work. The terms are not new to you; they are part of everyday vocabulary. However, they have definitions and meanings in physics that are different from those of day-to-day life. In common usage, energy refers to resources that are capable of producing energy—physical entities such as natural gas, oil, or coal. In physics, energy is not a substance, but rather a property of a physical system.
Energy can be defined as the capacity for doing work. As energy changes from one form to another, part of the available energy is transformed into work. This intertwined relationship is described by the work–energy theorem, a cornerstone of physics. The theorem states that work done on a system by an external force increases the energy of the system and that energy can be used to do work.
If an object moves under the influence of an external force, a physicist would say that work is done on the object by the force. If the object does not move, no work is done, no matter how large the force applied. So the important thing to remember is that in physics, an object must move a distance for work to be done. You may spend the whole afternoon pushing your car trying to get it out of the snow and finally decide that you have done enough work for the day. But if the car has not moved from where it was at the beginning, a physicist would have to conclude that no work was done on the car at all!
Figure 7.1: A block moves a distance $d$ under the influence of a constant force $F$.
By definition, work is equal to the product of force and the distance traveled. To represent work in a more mathematical form, consider the block in Figure 7.1. While the horizontal force $F$ is applied, the block moves a distance $d$ in the horizontal direction. The work $W$ done on the block is given as \begin{align} \text{Work} &= \text{force} \times \text{distance} \nonumber\\[6pt] \Rightarrow\quad W &= F d \end{align}
To say that work is done on an object, three conditions must be met:
- a force must be applied,
- the object must be displaced from its initial position, and
- the displacement must not be perpendicular to the direction of the applied force.
Note that the force of gravity ($mg$) does not do work on the block in Figure 7.1.
Gravitational Potential Energy
Figure 7.2: A block displaced a vertical distance $h$ above a tabletop by the minimum force required.
Suppose a block of mass $m$ is at rest on a tabletop, as shown in Figure 7.2. To lift the block, you must exert sufficient force ($F$) in the upward direction to overcome the downward force of gravity. So the minimum required force is equal to the weight of the block—in other words, $F = mg$. In this case, the net vertical force on the block is equal to zero, so it rises steadily without acceleration. If the block is displaced a vertical distance $h$ above its initial position on the tabletop, the work done on the block by the upward force is stored in the form of gravitational potential energy (PE). This is expressed mathematically as \begin{align} \text{Gravitational potential energy} &= \text{weight} \times \text{height} \nonumber\\[6pt] \Rightarrow\quad \text{PE} &= mg \times h \nonumber\\[6pt] &= mgh \end{align}
Kinetic Energy
The kinetic energy (KE) of a moving object is defined as half its mass multiplied by the square of its speed, or \begin{align} \text{Kinetic energy} &= \tfrac{1}{2}\, \text{mass} \times \text{speed}^2 \nonumber\\[6pt] \Rightarrow\quad \text{KE} &= \tfrac{1}{2} m v^2 \end{align}
Work–Energy Theorem
When a net external force $F$ acts on an object over a distance $d$, the kinetic energy of the object changes by an amount equal to the work done, or
\begin{align} \text{Work done} &= \text{change in kinetic energy} \nonumber\\[6pt] \Rightarrow\quad W &= \Delta\text{KE} \nonumber\\[6pt] \Rightarrow\quad F d &= \Delta (\tfrac{1}{2} m v^2) \label{ch07_we} \end{align}
Equations 7.4 show the relationship of work and energy in the work–energy theorem.
Conservation of Energy
One of the most celebrated laws of physics is the law of conservation of energy. The popular version states that energy can be neither created nor destroyed. A physicist may say the same thing in a different way:
The total energy of an isolated system is constant.
Figure 7.3: An object shot up with initial vertical velocity $v$.
Consider the object of mass $m$ shown in Figure 7.3, which is projected straight up from the ground level with an initial speed $v$. In the absence of wind and air resistance, the total energy ($\text{KE} + \text{PE}$) of the object remains unchanged while in free fall. This can be expressed as \begin{equation} \text{Mechanical energy} = \text{KE} + \text{PE} = \text{constant} \end{equation} In particular, the energy of the object near the ground level is given by \begin{align} \text{Energy near ground level} &= \frac{1}{2} m v^2 + 0 \nonumber\\[6pt] &= \frac{1}{2} m v^2 \end{align}
As the object rises, it loses kinetic energy and gains potential energy by an equal amount. When all the kinetic energy is converted into gravitational potential energy at the maximum height $h$, the object momentarily stops and you can write \begin{align} \text{Energy at maximum height} &= 0 + mgh \nonumber\\[6pt] &= mgh \end{align}
So you see that the total energy of the object does not change as it moves up against gravity; it is always equal to the amount of energy the object had at the start of the motion. When the object falls back after reaching the maximum height, its total energy is also conserved. In this case, however, potential energy is converted to kinetic energy until the object hits the ground with the same speed as its initial speed. You can relate the object’s initial speed and maximum height as follows: \begin{align} \text{Energy at maximum height} &= \text{energy near ground level} \nonumber\\[6pt] \Rightarrow\quad mgh &= \frac{1}{2} m v^2 \nonumber\\[6pt] \Rightarrow\quad h &= \frac{v^2}{2g} \end{align}
Video 7.1: Work and energy concepts.
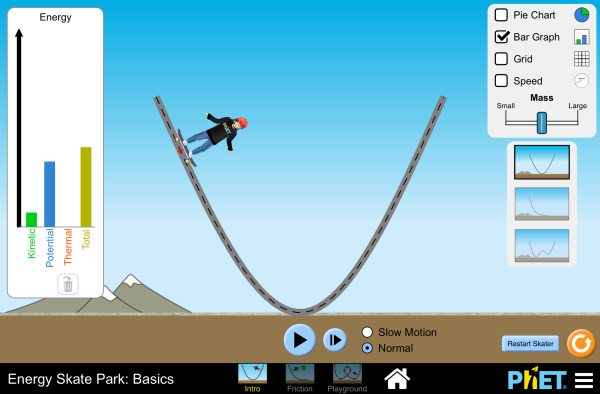
Simulation
Run the Energy Skate Park simulation to explore kinetic energy, potential energy, and friction as a skateboarder travels on different types of ramps.
Simulation by PhET Interactive Simulations, University of Colorado Boulder, licensed under CC-BY-4.0 (https://phet.colorado.edu)
Questions
The following questions are selected from the end of Chapter 7 of the eText. It is important to your learning that you try to answer each question independently before you read through the answer and explanation given.
For questions that ask you to explain or discuss your answer, the response revealed by the Answer button would earn you only partial marks on a quiz or exam in this course. Use the Answer to help you formulate a complete answer before you select the Explanation button to check your work.
Note that some questions have been adapted to suit the format of this course.
Chapter 7
Question 5
Which requires more work—lifting a 50-kg sack vertically 2 m or lifting a 25-kg sack vertically 4 m?
Answer
The same amount of work is required in both cases.
Explanation
To lift an object at a constant speed, you must apply an upward lifting force equal to the weight of the object. For the two sacks in this question, the minimum forces required are \begin{equation} F_1 = 50\,\text{kg}\times g = 500\,\text{N} \end{equation} and \begin{equation} F_2 = 25\,\text{kg}\times g = 250\,\text{N} \end{equation} The work required to lift each sack is equal to the applied vertical force multiplied by the corresponding vertical displacement, which is calculated as follows: \begin{align} \text{Work on sack 1} &= 500\,\text{N}\times 2\,\text{m} \nonumber\\[6pt] &= 1000\,\text{J} \end{align} and \begin{align} \text{Work on sack 2} &= 250\,\text{N}\times 4\,\text{m} \nonumber\\[6pt] &= 1000\,\text{J} \end{align}
Chapter 7
Question 17
If you push a crate horizontally with 100 N across a 10-m factory floor and friction between the crate and the floor is a steady 70 N, how much kinetic energy is gained by the crate?
Answer
300 J
Diagram
Figure Q7.17
Explanation
Based on the work–energy theorem, the net work done on the crate is equal to the change in its kinetic energy ($\Delta \text{KE}$). For the situation in this question (see Figure Q7.17), you have \begin{align} \Delta \text{KE} &= \text{net work} \nonumber\\[6pt] &= \text{net force} \times \text{distance} \nonumber\\[6pt] &= (100\,\text{N} - 70\,\text{N}) \times 10\,\text{m} \nonumber\\[6pt] &= 30\,\text{N} \times 10\,\text{m} \nonumber\\[6pt] &= 300\,\text{J} \end{align}
Chapter 7
Question 20
A peach hanging from a limb has potential energy because of its height. If it falls, what becomes of this energy just before it hits the ground? When it hits the ground?
Answer
The initial potential energy transforms into kinetic energy during the fall, then into heat when the peach hits the ground.
Explanation
While the peach is falling toward the ground, the force of gravity does work on the peach, increasing its kinetic energy. Almost all the initial gravitational potential energy converts into kinetic energy just before the peach hits the ground. A small amount of the total energy appears as heat due to air drag during the fall.
On impact, the majority of the peach’s kinetic energy transforms into thermal energy—the peach and the ground warm up a little. A small amount of the energy is carried by the sound waves that you hear upon impact.
Chapter 7
Question 22
Can a machine multiply input force? Input distance? Input energy? (If your three answers are the same, seek help, for the last question is especially important.)
Answer
A machine can multiply input force or input distance, but not input energy.
Explanation
A specific amount of input energy can cause a machine to do a certain amount of work. The output force and distance, however, may vary, but their multiplication remains equal to the work done. For example, the machine can produce a small force that acts over a relatively long distance, or it can apply a large force over a shorter distance. It is important to note that a machine does not create energy. Therefore, output energy cannot exceed input energy.
Chapter 7
Question 24
A force of 50 N is applied to the end of a lever, which is moved a certain distance. If the other end of the lever moves one-third as far, how much force can it exert?
Answer
150 N
Explanation
The input work done at the end of the lever is equal to \begin{equation} F_\text{input} \times \text{distance} = 50\,\text{N} \times \text{distance} \end{equation} while the output work at the other end is given by \begin{equation} F_\text{output} \times \left(\frac{\text{distance}}{3}\right) \end{equation} Since energy is conserved, output work is equal to input work and you can calculate the maximum force exerted by the lever as follows: \begin{align} \text{Output work} &= \text{input work} \nonumber\\[6pt] \Rightarrow\quad F_\text{output} \times \left(\frac{\text{distance}}{3}\right) &= 50\,\text{N} \times \text{distance} \nonumber\\[6pt] \Rightarrow\quad F_\text{output} &= 3 \times 50\,\text{N} \nonumber\\[6pt] &= 150\,\text{N} \end{align}
Chapter 7
Question 25
What is the efficiency of a machine that miraculously converts all the input energy to useful output energy?
Answer
100%
Explanation
This perfect machine works at the maximum efficiency of \begin{equation} \frac{\text{Useful energy output}}{\text{Total energy input}} = 1 \end{equation}
Chapter 7
Question 28
What is the ultimate source of energy for fossil fuels, dams, and windmills?
Answer
The Sun.
Explanation
Fossil fuels (coal and oil) were formed from remains of plants and other organisms on Earth hundreds of millions of years ago. As you know, visible light from the Sun is essential for photosynthesis, which causes plants to grow.
Rivers flow because of global water circulation powered by the Sun, which continuously vaporizes water from oceans and lakes and stores it in clouds. When rain falls on mountains, rivers flow and fill reservoirs behind dams.
Nonuniform heating of Earth’s surface by the Sun creates geographical differences in atmospheric pressure, which cause the winds to blow.
Chapter 7
Question 46
How much work is required to lift a 250-kg appliance to the second-story level of a house 6.0 m above street level?
Answer
15 kJ
Explanation
In this case, the movers must exert an upward force that is at least equal to the appliance’s weight: \begin{align} \text{Weight} &= (250\,\text{kg}) \, (10\,\text{m}/\text{s}^2) \nonumber\\[6pt] &= 2500\,\text{N} \end{align} Assuming a constant upward force, the work done on the appliance is calculated as \begin{align} \text{Work} &= (2500\,\text{N}) \, (6\,\text{m}) \nonumber\\[6pt] &= 15{,}000\,\text{J} \quad (\text{or}\; 15\,\text{kJ}) \end{align}
Chapter 7
Question 47
This is typical driver’s license question: A car moving at 50 km/h skids 15 m with locked brakes. How far will the car skid with locked brakes at 150 km/h? (Or, translate this to how far at 3 times the speed?)
Answer
135 m
Explanation
A car (of mass $m$) stops when its kinetic energy dissipates as heat due to the work done by the force of friction between the locked tires and the road. For this question, you can assume the force of friction ($F$) depends on the road and tire conditions only, independent of the car’s speed. Therefore, at both speeds mentioned in the question, the car experiences the same force while skidding.
By applying the work–energy theorem to the car traveling at an initial speed of 50 km/h, you can write
\begin{equation} F \times 15\,\text{m} = \frac{1}{2} m\, (50\,\text{km/h})^2 \label{ch07_q43_50} \end{equation}
The same car traveling at an initial speed of 150 km/h skids for a distance $d$ before stopping. Using the work–energy theorem, you have
\begin{align} F d &= \frac{1}{2} m\, (150\,\text{km/h})^2\nonumber\\[6pt] \Rightarrow\quad F d &= \frac{1}{2} m\, (3 \times 50\,\text{km/h})^2 \nonumber\\[6pt] \Rightarrow\quad F d &= 9 \times \frac{1}{2} m\, (50\,\text{km/h})^2 \label{ch07_q43_150} \end{align}
You can now substitute from Equation 7.20 into Equation 7.21 and calculate the distance $d$ as follows: \begin{align} F d &= 9 \times \left(F \times 15\,\text{m}\right) \nonumber\\[6pt] \Rightarrow\quad d &= 9 \times 15\,\text{m} \nonumber\\[6pt] \Rightarrow\quad d &= 135\,\text{m} \end{align} So when the speed triples, the stopping distance increases by nine times!
Chapter 7
Question 52
In the hydraulic machine shown, when the small piston is pushed down 10 cm, the large piston is raised 1 cm. If the small piston is pushed down with a force of 100 N, what is the most weight that the large piston can support?
Figure Q7.52(a)
Answer
1000 N
Diagram
Figure Q7.52(b)
Explanation
This machine, sometimes called a hydraulic lever, transmits the pressure undiminished from one end to the other. According to the law of conservation of energy, the input work done on the small piston is equal to the output work performed by the large piston, which is expressed mathematically as \begin{align} (\text{force} \times \text{distance})_\text{input} &= (\text{force} \times \text{distance})_\text{output} \nonumber\\[6pt] \Rightarrow\quad 100\,\text{N} \times 10\,\text{cm} &= \text{weight} \times 1\,\text{cm} \end{align} Assuming 100% efficiency, you can calculate the maximum weight that the large piston can support as follows: \begin{align} \text{Weight} &= \frac{100\,\text{N} \times 10\,\text{cm}}{1\,\text{cm}} \nonumber\\[6pt] &= 10 \times 100\,\text{N} \nonumber\\[6pt] &= 1000\,\text{N} \end{align}
Chapter 7
Question 53
How many watts of power do you expend when you exert a force of 50 N that moves a crate 6.0 m in 3.0 s?
Answer
100 W
Explanation
The work done on the crate is equal to \begin{equation} 50\,\text{N}\times 6.0\,\text{m} = 300\,\text{J} \end{equation} Since power is the work done (or energy spent) per second, you can write \begin{align} \text{Power} &= \frac{\text{work}}{\text{time}} \nonumber\\[6pt] &= \frac{300\,\text{J}}{3.0\,\text{s}} \nonumber\\[6pt] &= 100\,\text{W} \end{align}
Chapter 7
Question 64
Why does one get tired when pushing against a stationary wall when no work is done on the wall?
Answer
Work is done inside the muscles of the person pushing against the wall.
Explanation
Muscles consist of thousands of thin fibers that contract and relax quickly, even if this does not produce limb movement, such as when pushing against a stationary wall. No work is done on the wall, but a lot of work is done by the muscles inside the body, which causes them to eventually fatigue.
Chapter 7
Question 80
A ball is thrown straight up in the air.
- Where in its path is its kinetic energy at a maximum?
- Where is its gravitational potential energy at a maximum?
Answer
- Kinetic energy is at its maximum at the instant the ball leaves the thrower’s hand.
- Gravitational potential energy is at its maximum at the highest point of the ball’s ascent.
Diagram
Figure Q7.80
Explanation
- The ball starts at rest in the thrower’s hand. The thrower’s hand then exerts an upward force on the ball greater than the ball’s weight. As a result, the ball accelerates upward and reaches maximum speed (or greatest kinetic energy) as it leaves the thrower’s hand (see Figure Q7.80).
- While in the air, the ball experiences free fall under the influence of gravity alone. During the upward stage of its motion, the ball slows down uniformly until it stops momentarily at the highest point. At this instant, the ball has zero kinetic energy and its gravitational potential energy is at its maximum value.
Chapter 7
Question 87
If your momentum is zero, is your kinetic energy necessarily zero also?
Answer
Yes, if you are moving as a single body.
Explanation
For a single rigid object, zero momentum means zero speed and zero kinetic energy. However, a system of two or more bodies or objects can have zero net momentum while the different components of the system move and contribute to the system’s total kinetic energy. An example is a warm container filled with air that is sitting on a tabletop. In this case, the net momentum of the container is equal to zero, but the total kinetic energy of the air molecules inside it is relatively large.
Chapter 7
Question 90
An inefficient machine is said to “waste energy.” Does this mean that energy is actually lost? Explain.
Answer
No.
Explanation
In this context, “to waste energy” means the machine transforms only a small fraction of energy input into useful forms of energy output. The remainder is wasted in forms of energy considered nonbeneficial. A machine, of course, cannot destroy energy.
Chapter 7
Question 92
Your friend says that one way to improve air quality in a city is to have traffic lights synchronized so that motorists can travel long distances at constant speed. What physics principle supports this claim?
Answer
The law of conservation of energy.
Explanation
Ideally speaking, in the absence of friction and air resistance, a car would continue to move in the same direction and at a constant speed even if the engine were turned off (see Newton’s first law). In a real situation, when a car cruises at a constant speed, the engine works just to compensate for the energy lost due to air drag.
However, every time the driver stops the car at a traffic light, the initial kinetic energy of the car transforms entirely into heat energy through the work done by the braking system. When the light changes and the car pulls away, extra fuel must be burned to accelerate the car and regain the desired kinetic energy. Therefore, when cars must stop frequently at traffic lights, there is a significant increase in gas consumption, which is an important contributor to air pollution.
Chapter 7
Question 99
If a golf ball and a ping-pong ball both move with the same kinetic energy, can you say which has the greater speed? Explain in terms of the definition of KE. Similarly, in a gaseous mixture of heavy and light molecules with the same average KE, can you say which have the greater speed?
Answer
The ping-pong ball has a greater speed than the golf ball, and lighter molecules move faster than heavier ones in a gaseous mixture.
Explanation
Recall the formula for kinetic energy: \begin{align} \text{KE} &= \frac{1}{2} m v^2 \nonumber\\[6pt] \Rightarrow\quad v &= \sqrt{\frac{2\, \text{KE}}{m}} \end{align} When two objects have the same kinetic energy, the heavier object (the golf ball in this case) moves slower than the lighter one (the ping-pong ball).
Similarly, you can argue that the lighter molecules in a gaseous mixture move faster than the heavier molecules, which have the same average kinetic energy.
Chapter 7
Question 104
In the absence of air resistance, a ball thrown vertically upward with a certain initial KE will return to its original level with the same KE. When air resistance is a factor affecting the ball, will it return to its original level with the same, less, or more KE? Does your answer contradict the law of energy conservation?
Answer
The ball will return with less KE, and this does not contradict the law of energy conservation.
Explanation
The decrease in the ball’s kinetic energy when the ball returns to its original vertical position is caused by the work done on the ball by the force of air resistance, which always acts opposite to the direction of motion. The air resistance converts part of the ball’s mechanical energy into heat, so the law of energy conservation is not violated.
Chapter 7
Question 107
Going uphill, the gasoline engine in a hybrid electric car provides 75 horsepower while the total power propelling the car is 90 horsepower. Burning gasoline provides the 75 horsepower. Discuss what provides the other 15 horsepower.
Hint
Consider that gasoline was burned at an earlier time but not used to drive the car.
Answer
While idling or going downhill, a hybrid car burns gasoline to charge its electric battery, which is a part of a hybrid engine. The charged battery provides driving power (15 horsepower in this case) to assist the gasoline engine when required. The benefit of a hybrid engine is that it is more efficient than a regular gasoline engine.
Chapter 7
Question 115
When an electric company can’t meet its customers’ demand for electricity on a hot summer day, is this an “energy crisis” or a “power crisis”? Discuss.
Hint
Think about the difference between the total energy produced by the electric company in one day and the maximum energy that can be delivered to customers in one hour.
Answer
The problem here is that the electric company can’t produce energy at a sufficient rate during a period of high demand. Since “power” refers to the amount of energy produced or delivered per unit time, “power crisis” is a more accurate description of the situation in this question.
Additional Questions
Answer the following additional questions (not found in your eText).
Unit 7
Question A
Two blocks are lifted from the floor and placed to the same shelf. One block is twice as massive as the other. Compare their gains of potential energy.
Answer
The block that is twice as massive has twice as much potential energy as the other block.
Hint
When raised to an elevation $h$ above the ground, an object of mass $m$ gains gravitational potential energy as given by the equation \begin{equation} \text{PE} = mgh \end{equation} The potential energy is proportional to the mass of the raised object. So if the elevation is kept constant, doubling the mass also doubles the potential energy. Another way to look at this problem is to think of the heavier block as two lighter blocks raised together to the same elevation.
Unit 7
Question B
When a commercial airplane slows down, then lands in an airport, large amounts of kinetic and potential energy are lost. Where does the energy go?
Answer
The kinetic energy and potential energy are converted primarily to heat.
Hint
Work done by air resistance transforms the mechanical (kinetic and potential) energy of the airplane into heat, which results in an increase of the temperature of the plane’s body and surrounding air. (Note that a shooting star is a piece of rock that burns because of the intense heat generated when it rubs air molecules in Earth’s atmosphere.) A small fraction of the initial mechanical energy is converted to the sound waves you hear as the plane lands.
Unit 7
Question C
How much work is done on a satellite in circular orbit?
Answer
No work is done on the satellite, whose speed remains constant.
Diagram
Figure E7.C
Explanation
As the satellite moves along a circular orbit (see Figure E7.C), the force of gravity ($F_g$) continuously acts perpendicular to the satellite’s velocity ($v$). In this case, $F_g$ is actually the centripetal force responsible for the uniform circular motion. Since the satellite does not perform any displacement in the direction of the applied force, no work is done by the force of gravity on the satellite, whose kinetic energy (and speed) does not change with time.
Unit 7
Question D
Two cars with equal and opposite momenta are involved in a head-on collision and come to rest. What physical quantities are conserved or not conserved in this accident?
Answer
Momentum is conserved, but kinetic energy is not conserved.
Hint
Initially, the two cars move with equal and opposite momenta, so the total momentum of the system before the collision is equal to zero. After the collision, the vehicles stick together and come to rest (zero final momentum).
The total kinetic energy of the two-car system is equal to the sum of the kinetic energies of the moving cars. After the accident, the cars stop moving and their individual kinetic energies become zero. So, during impact, the initial kinetic energies transform into heat (i.e., kinetic energy of molecular motion). Note, however, that the total energy of the system is conserved.
Unit 7
Question E
Why it is more fuel efficient to close the windows of a car traveling at higher speeds?
Answer
Open windows on a car traveling at relatively high speeds cause a significant increase in air drag.
Hint
Opening the windows of a moving car causes turbulent movement of the air inside the car and the surrounding air. This reduces the streamlined movement of the air around the vehicle, significantly increases air drag, especially at higher speeds. So, to maintain your speed, you must step on the gas more, which causes the car to consume more fuel than it would if the windows were closed.
Exercises
Spend some time completing the following exercises to test your understanding of the main concepts in Chapter 7 and increase your efficiency in answering exam questions.
End-of-Chapter Practice Questions
Answer questions 3, 7, 11, 21, 25, 29, 31, 35, 37, 39, 43, 51, 55, 57, 59, 63, 73, 83, 85, 91, 101, 109, and 111 in Chapter 7 of the eText. If you require assistance, please contact your tutor. The answers are provided at the end of the eText.