Unit 4: Newton’s Second Law of Motion
On the Moon, you weigh 83% less than on Earth, but your mass remains the same. After completing this unit, you should be able to explain the difference between mass and weight in physics.
Learning Outcomes
By the end of this unit, you should be able to
- discuss the relation between the net force on an object and the object’s acceleration.
- give examples of situations and scenarios involving forces of friction.
- write and explain the mathematical representation of Newton’s second law of motion.
- define terminal speed and explain how air drag affects the acceleration of a falling object.
eText Material
Reading Assignment
Read the following sections in Chapter 4 of the eText:
- 4.1: Forces
- 4.2: Friction
- 4.3: Mass and Weight
- 4.4: Newton’s Second Law of Motion
- 4.5: When Acceleration Is $g$—Free Fall
- 4.6: When Acceleration Is Less Than $g$—Nonfree Fall
Supplementary learning resources are available on the Mastering Physics learning platform.
Additional Reading
Friction and Drag
The term friction refers to one of the most common resistive forces you experience on a daily basis. Suppose you give a push to a book on a horizontal tabletop. If there were no friction, the book would continue to slide without losing its speed. Also, experience tells you that moving a piece of furniture over a polished surface is much easier than over carpet. This is because the force of friction between the furniture and the carpet is much larger than the force of friction between the same piece of furniture and a polished floor.
Interestingly, mobility is sometimes possible because of friction. For example, you can walk safely because of the friction between the ground and the soles of your shoes. Also, without friction, a car’s tire would spin in the same spot without causing any forward motion.
Surface imperfections can be thought of as the cause of friction. When two surfaces are in contact, the tiny protrusions of their imperfections push against one another, opposing the motion of one surface over the other. Although this model is quite simple, it allows you to visualize why the strength of frictional forces depends on the material and roughness of the surfaces in contact and how much they are pressed against each other.
A solid object moving through a fluid (liquid or gas) also experiences a resistive force called drag. Unlike the friction between solid dry surfaces, drag (or fluid friction) depends on speed. This explains why the engine works harder when an automobile cruises at a higher speed.
Mass and Weight
The words mass and weight are frequently treated as synonyms in everyday use. In physics, however, the two words describe different physical quantities. Mass quantifies the amount of matter in an object, while weight refers to the force of gravity on the object. Therefore, a piece of rock has the same mass on Earth, the Moon, Mars, or anywhere in the universe. The weight of the rock, however, differs from one celestial body to another depending on the acceleration due to gravitation experienced by the rock.
Newton’s Second Law of Motion
Newton’s second law of motion provides a more precise definition of force in terms of its capacity to cause acceleration. From experience, you know that larger forces cause greater accelerations. More specifically, if the net force ($F_\text{net}$) applied on an object is doubled, its acceleration will be doubled, and if the net force is tripled, the acceleration will be tripled too, and so on. The acceleration ($a$) is therefore said to be proportional to the net applied force.
Now consider what happens when you apply equal forces on two objects, one heavier than the other. Once again, you know from experience that the heavier object will experience less acceleration than the lighter one. With careful measurements, you will find that if the mass ($m$) is doubled, the acceleration is reduced by one-half, and it becomes one-third if the mass is tripled without changing the applied force. Therefore, the mathematical relationship between $a$, $F_\text{net}$, and $m$ can be expressed as \begin{equation} a = \frac{F_\text{net}}{m} \end{equation} or \begin{equation} F_\text{net} = ma \end{equation} The formula above is the mathematical form of Newton’s second law of motion.
The unit of measurement for force is called the newton, abbreviated as N. The newton is defined such that a force of 1 N acting on an object of mass 1 kg produces an acceleration of 1 m/s2.
Video 4.1: Newton’s second law of motion.
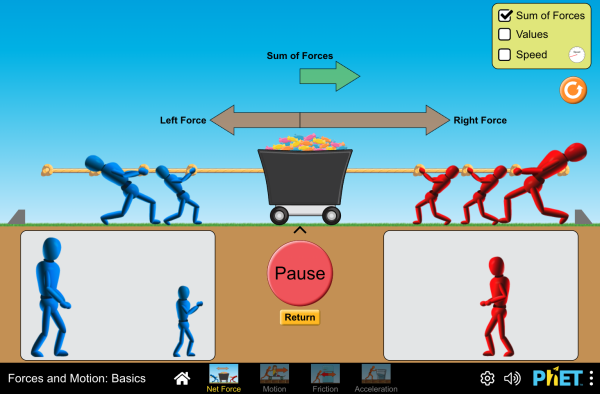
Simulation
Run the Forces and Motion simulations to explore the interaction of forces and friction on the motion of an object.
Simulation by PhET Interactive Simulations, University of Colorado Boulder, licensed under CC-BY-4.0 (https://phet.colorado.edu)
Questions
The following questions are selected from the end of Chapter 4 of the eText. It is important to your learning that you try to answer each question independently before you read through the answer and explanation given.
For questions that ask you to explain or discuss your answer, the response revealed by the Answer button would earn you only partial marks on a quiz or exam in this course. Use the Answer to help you formulate a complete answer before you select the Explanation button to check your work.
Note that some questions have been adapted to suit the format of this course.
Chapter 4
Question 3
When a crate is pushed horizontally and doesn’t slide along a level floor, how great is the force of friction on the crate?
Answer
The force of friction is equal to the applied force.
Diagram
Figure Q4.3
Explanation
Since the crate doesn’t slide, its acceleration is equal to zero. Hence, the net force on the crate is also equal to zero. As shown in Figure Q4.3, the force of friction has exactly the same magnitude (but opposite direction) as the force applied on the crate.
Chapter 4
Question 6
How does the force of friction for a sliding object vary with speed?
Answer
It does not vary with speed.
Explanation
At the microscopic level, frictional forces between two dry surfaces sliding and rubbing against each other are quite complicated. However, for most practical purposes, the force of friction can be considered independent of the speed and the area of contact between the two surfaces. So varying the speed does not change the force of friction on a sliding object.
Chapter 4
Question 8
Which is more fundamental, mass or weight? Which varies with location?
Answer
Mass is more fundamental and is independent of location.
Explanation
Mass is an intrinsic property and represents the quantity of matter in an object. A 10-kg rock has the same mass everywhere—on Earth, on the Moon, or in deep space far from any planet or star. Also, note that mass ($m$) is a scalar quantity.
Weight, however, is a vector quantity and represents the force of gravity on an object. Numerically, the magnitude of an object’s weight ($mg$) is equal to the product of its mass and the acceleration due to gravity at the location of the object. Since the gravitational force deceases with altitude, the same object weighs less at the top of a mountain than near sea level.
The mass of a spacesuit (without the astronaut in it) is more than 120 kg, which corresponds to a weight of 1200 N on Earth. On the surface of the Moon, however, the spacesuit s weight reduces to about 200 N. Its mass, of course, remains the same.
Chapter 4
Question 12
What is the weight in newtons of a 1-kilogram brick resting on a table?
Answer
10 N
Explanation
The weight of a 1-kilogram brick is equal to the force on it due to gravity, or \begin{align} \text{Weight} &= m g \nonumber\\[6pt] &= (1\,\text{kg})\, (10\,\text{m}/\text{s}^2) \nonumber\\[6pt] &= 10\,\text{N} \end{align}
Chapter 4
Question 18
If the net force acting on a sliding block is somehow doubled, what happens to the acceleration?
Answer
The acceleration doubles.
Explanation
Newton’s second law of motion can be expressed in the form \begin{equation} a = \left(\frac{1}{m}\right) F \end{equation} Based on this equation, the acceleration ($a$) of a sliding block is proportional to the net applied force ($F$). In other words, if the net force applied on the block is doubled, its acceleration is also doubled. Similarly, if $F$ is tripled, $a$ increases to three times the initial value. Note that the mass of the block ($m$) is constant in this situation.
Chapter 4
Question 28
What is the acceleration of a falling object that has reached its terminal velocity?
Answer
Zero.
Explanation
An object reaches terminal velocity when it stops accelerating and continues to fall down at a constant speed. In such a state, the upward force due to air drag balances the downward force due to gravity (or the object’s weight). As a result, the net force on the falling object is equal to zero.
Chapter 4
Question 30
If two objects of the same size fall through the air at different speeds, which encounters the greater air resistance?
Answer
The faster object.
Explanation
Air resistance depends on the speed, size, and shape of an object. The resulting drag force increases with the object’s size and speed. If two objects have the same size (and shape), the faster object encounters greater air resistance.
Chapter 4
Question 41
What is the net force acting on a falling 1-kg ball if it encounters 2 N of air resistance?
Answer
8 N, downward
Diagram
Figure Q4.41
Explanation
As shown in Figure Q4.41, two forces act on the falling ball: the force of gravity ($mg$) directed downward and the force of air resistance ($R$), which acts upward, opposite to the direction of motion. So you have \begin{align} mg &= (1\,\text{kg})\, (10\,\text{m}/\text{s}^2) \nonumber\\[6pt] &= 10\,\text{N}\quad (\text{downward}) \end{align} and \begin{equation} R = 2\,\text{N}\quad (\text{upward}) \end{equation} The net force on the ball is then equal to the difference between its weight and the force of air resistance: \begin{align} F_\text{net} &= mg - R \nonumber\\[6pt] &= 10\,\text{N} - 2\,\text{N} \nonumber\\[6pt] &= 8\,\text{N}\quad (\text{downward}) \end{align}
Chapter 4
Question 44
A 40-kg block of cement is pulled sideways with a net force of 200 N. Show that its acceleration is $5\,\text{m}/\text{s}^2$.
Answer
By applying Newton’s second law of motion, you can calculate the acceleration of the block as follows: \begin{align} a &= \frac{F_\text{net}}{m} \nonumber\\[6pt] &= \frac{200\,\text{N}}{40\,\text{kg}} \nonumber\\[6pt] &= 5\,\text{m}/\text{s}^2 \end{align}
Chapter 4
Question 62
Because an object weighs less on the surface of the Moon than on Earth’s surface, does it have less inertia on the Moon’s surface?
Answer
No.
Explanation
Inertia is a synonym for mass, which is a measure of the amount of material in an object. Relocating an object does not affect its composition—it will have the same mass anywhere. Thus, an object’s inertia on the Moon is the same as on Earth.
Chapter 4
Question 65
In an orbiting space vehicle, you are handed two identical boxes, one filled with sand and the other filled with feathers. How can you determine which is which without opening the boxes?
Answer
Observe how the boxes respond to an applied force.
Explanation
Push the two boxes simultaneously with equal forces, using your left hand on one and your right on the other. The lighter box (filled with feathers) will have greater acceleration and move faster than the heavier box (filled with sand).
Chapter 4
Question 85
A friend says that as long as a car is at rest, no forces act on it. What do you say if you’re in the mood to correct the statement of your friend?
Answer
I would say, “You mean that no net force acts on the car!”
Diagram
Figure Q4.85
Explanation
A car parked on a steep road, for example, experiences multiple forces, as shown in Figure Q4.85. First, there is the force of gravity (or weight), which acts in the downward direction. The second force on the car is called the normal (or support) force, and it is exerted perpendicular to the road’s surface. The car is prevented from sliding down the road by the force of friction, which is directed up the slope. These three forces, however, add up to zero. Your friend’s statement can be corrected by saying, “As long as a car is at rest, it experiences zero net force.”
Chapter 4
Question 90
How does the force of gravity on a raindrop compare with the air drag it encounters when it falls at constant velocity?
Answer
Both forces are equal in strength.
Explanation
Constant velocity means zero acceleration. According to Newton’s second law, the net force on the raindrop when it reaches terminal velocity must be equal to zero. Thus, the downward force of gravity on the raindrop is equal in magnitude to the upward force of air drag.
Chapter 4
Question 91
When a falling parachutist at terminal speed opens her parachute, in what direction does she accelerate?
Answer
Upward.
Explanation
When the parachute opens, the upward force of air resistance on the parachutist sharply increases and becomes much greater than her weight (downward force of gravity). As a result, the parachutist experiences a net force in the upward direction and starts to slow down—or, in other words, accelerate upward. As the falling speed decreases, air drag also becomes smaller. A new terminal speed is achieved when the force of air resistance becomes equal to the parachutist’s weight.
Chapter 4
Question 97
When and if Galileo dropped two balls of the same size but different masses from the top of the Leaning Tower of Pisa, air resistance was not really negligible. Which ball actually struck the ground first? Why?
Answer
The more massive ball.
Explanation
Assume Galileo dropped two solid balls of equal diameters, one made of steel and the other of wood. In this case, the downward force of gravity ($m_\text{s}\,g$) on the steel ball is much larger than the force of gravity ($m_\text{w}\,g$) on the lighter wooden ball.
Since the two balls have the same shape and size, the upward force ($R$) of air drag will depend on speed only. So, initially, the steel ball will experience greater downward acceleration ($g - R/m_\text{s}$) compared with the acceleration ($g - R/m_\text{w}$) of the wooden ball. Also, the steel ball will have to gain a much higher speed than the wooden ball before it reaches terminal velocity. So, overall, the heavier steel ball moves faster and strikes the ground first.
Chapter 4
Question 106
Is it possible to move in a curved path in the absence of a force? Discuss why.
Answer
No.
Explanation
Velocity is a vector quantity, with magnitude and direction, and any change in the speed or direction of motion of an object requires acceleration. While moving on a curved path, an object continuously changes its direction of motion, which means it continuously accelerates. According to Newton’s second law, acceleration is not possible without an applied force.
Chapter 4
Question 110
Three identical blocks are pulled, as shown, on a horizontal frictionless surface. If the tension in the rope held by the hand is 30 N, discuss what the tension is in the other ropes.
Figure Q4.110(a)
Answer
10 N in the rope between the left block and the center block, and 20 N in the rope between the center block and the right block.
Diagram
Figure Q4.110(b)
Explanation
Since the three blocks (of mass $m$ each) are connected, they all move together with the same acceleration ($a$). According to Newton’s second law, the force pulling the first block from the left is given by $F = m a$. Also, you will need twice the force ($2F$) to accelerate two blocks and a force equal to $3F$ for all three blocks to have an acceleration $a$.
In Figure Q4.110(b), you see that the tension $T_1$ in the first rope accelerates a single block, while the tension $T_2$ in the second rope accelerates two blocks. Therefore, $T_2 = 2F$ has twice the value of $T_1 = F$. Similarly, the tension in the rope held by the hand is given as \begin{equation} T_3 = 3 F = 30\,\text{N} \end{equation} So, you have \begin{equation} F = \frac{30\,\text{N}}{3} = 10\,\text{N} \end{equation} and you can write \begin{equation} T_1 = F = 10\,\text{N} \end{equation} and \begin{equation} T_2 = 2F = 20\,\text{N} \end{equation}
Chapter 4
Question 118
Explain whether or not a sheet of paper falls more slowly than one that is wadded into a ball.
Answer
The flat sheet of paper falls more slowly.
Explanation
The masses and, consequently, the weights of the two sheets are equal. The flat sheet of paper, however, has greater surface area than the wadded one. As a result, when both have the same speed, the upward force of air resistance (or drag) on the flat sheet is greater than on the wadded one. Consequently, the flat sheet reaches terminal velocity more quickly and falls slower than the wadded one.
Chapter 4
Question 119
Upon which will air resistance be greater—a sheet of falling paper or the same paper wadded into a ball that falls at a faster terminal speed? (Careful!)
Answer
The air resistance is the same in both situations.
Explanation
The sheet of paper has the same weight whether it is flat or crumpled into a ball. However, when it is flat, the sheet of paper balances the forces (i.e., air drag equals the weight) at a smaller terminal speed than when the sheet is wadded into a ball. While falling at its terminal speed, an object always experiences zero net force, where the upward force of air resistance is equal to the downward force of gravity (or weight).
Exercises
Spend some time completing the following exercises to test your understanding of the main concepts in Chapter 4 and increase your efficiency in answering exam questions.
End-of-Chapter Practice Questions
Answer questions 5, 7, 15, 19, 21, 25, 29, 37, 39, 43, 51, 59, 63, 75, 77, 81, 83, 89, 99, and 109 in Chapter 4 of the eText. If you require assistance, please contact your tutor. The answers are provided at the end of the eText.