Unit 13: Liquids
A 60,000-ton cruise ship navigates steadily on the ocean surface for the same reason a plastic toy floats in a bathtub. After completing this unit, you should be able to explain how the buoyant force balances the immense weight of a large ship and prevents it from sinking.
Learning Outcomes
By the end of this unit, you should be able to
- explain the notion of liquid pressure.
- define buoyant force and state Archimedes’ principle.
- explain the role of density in the floating or sinking of an object.
- state Pascal’s principle.
- explain surface tension.
- explain capillarity.
eText Material
Reading Assignment
Read the following sections in Chapter 13 of the eText:
- 13.1: Pressure
- 13.2: Pressure in a Liquid
- 13.3: Buoyancy
- 13.4: Archimedes’ Principle
- 13.5: What Makes an Object Sink or Float?
- 13.6: Flotation
- 13.7: Pascal’s Principle
- 13.8: Surface Tension
- 13.9: Capillarity
Supplementary learning resources are available on the Mastering Physics learning platform.
Additional Reading
Water Pressure
One cubic centimeter of distilled water at 4°C has a mass of 1 g. If you combine 1000 cm3, you will have a total volume of 1 L. Therefore, a liter of water has a mass of 1 kg. Also, 1000 L (or 1000 kg) of water can fill a 1-m3 container. Since density is defined as mass per unit volume, you can write \begin{equation} \text{Density of water} = 1\,\text{g}/\text{cm}^3 = 1000\,\text{kg}/\text{m}^3 \end{equation} For comparison, the density of olive oil is 0.92 g/cm3, and for mercury it is 13.5 g/cm3. This is why oil floats on top of water, while mercury sinks to the bottom.
In terms of weight, 1 m3 of water experiences a downward force of gravity equal to \begin{equation} m_\text{water}\, g = (1000\,\text{kg}) (10\,\text{m}/\text{s}^2) = 10{,}000\,\text{N} \end{equation} So the weight density of water is equal to \begin{align} \frac{m_\text{water}\, g}{1\,\text{m}^3} = 10{,}000\,\text{N}/\text{m}^3 \end{align}
An object submerged under water experiences a pressure equal to the weight per unit area of the water column above the object. This can be expressed mathematically as \begin{align} \text{Water pressure} &= \text{weight density} \times \text{depth} \nonumber\\[6pt] &= 10{,}000\,\text{N}/\text{m}^3 \times \text{depth in meters} \end{align}
Buoyancy
Imagine a fictitious membrane enclosing a cube of water with a volume of 1 m3 deep in a lake. Each of the cube’s six faces experiences a water pressure based on the cube’s depth below the lake’s surface. The forces on the four side faces of the cube cancel each other, resulting in zero net force in the horizontal direction. However, the upward force on the bottom face is greater than the downward force on the top face because of the difference in depth. The resultant is an upward force on the water cube, called the buoyant force. Since the water cube is stable, the buoyant force must be equal to the cube’s weight ($m_\text{water}\, g$).
Now imagine you replace the water cube with a wooden block of the same shape and size. Since the surrounding water did not change, the buoyant force on the block remains equal to the weight of the water removed ($m_\text{water}\, g$). So you can calculate the net vertical force on the wooden block as follows: \begin{align} \text{Force}_\text{wood} &= \text{buoyant force} - \text{weight of wooden block} \nonumber\\[6pt] &= m_\text{water}\, g - m_\text{wood}\, g \nonumber\\[6pt] &= (m_\text{water} - m_\text{wood})\, g \end{align} Since wood has a lower density than water, $m_\text{wood}$ is less than $m_\text{water}$. Therefore, the wooden block experiences a net vertical force, which pushes the block upward to the water’s surface. You can use the same calculation to show why a block of steel sinks to the bottom of the lake.
Questions
The following questions are selected from the end of Chapter 13 of the eText. It is important to your learning that you try to answer each question independently before you read through the answer and explanation given.
For questions that ask you to explain, defend, or discuss your answer, the response revealed by the Answer button would earn you only partial marks on a quiz or exam in this course. Use the Answer to help you formulate a complete answer before you select the Explanation button to check your work.
Note that some questions have been adapted to suit the format of this course.
Chapter 13
Question 8
Why is there no horizontal buoyant force on a submerged object?
Answer
The pressure on an object at a specific point depends on its depth below the surface. The horizontal forces on a submerged object cancel out because every horizontal force that acts on one side of the object is countered by a force of equal magnitude that pushes on the opposite side at the same depth.
Chapter 13
Question 38
When a 1-m-tall barrel is filled with water, the pressure at the bottom of the barrel is 10 kPa. If you close the top and extend a thin empty 5-m-tall pipe on top, the pressure at the bottom of the barrel is still 10 kPa. If you then fill the pipe with water, the effective height of the water from the bottom of the barrel is 6 m. What is the pressure at the bottom of the barrel when water is added to fill the pipe to its top? (This activity sometimes bursts a barrel!)
Answer
60 kPa
Diagram
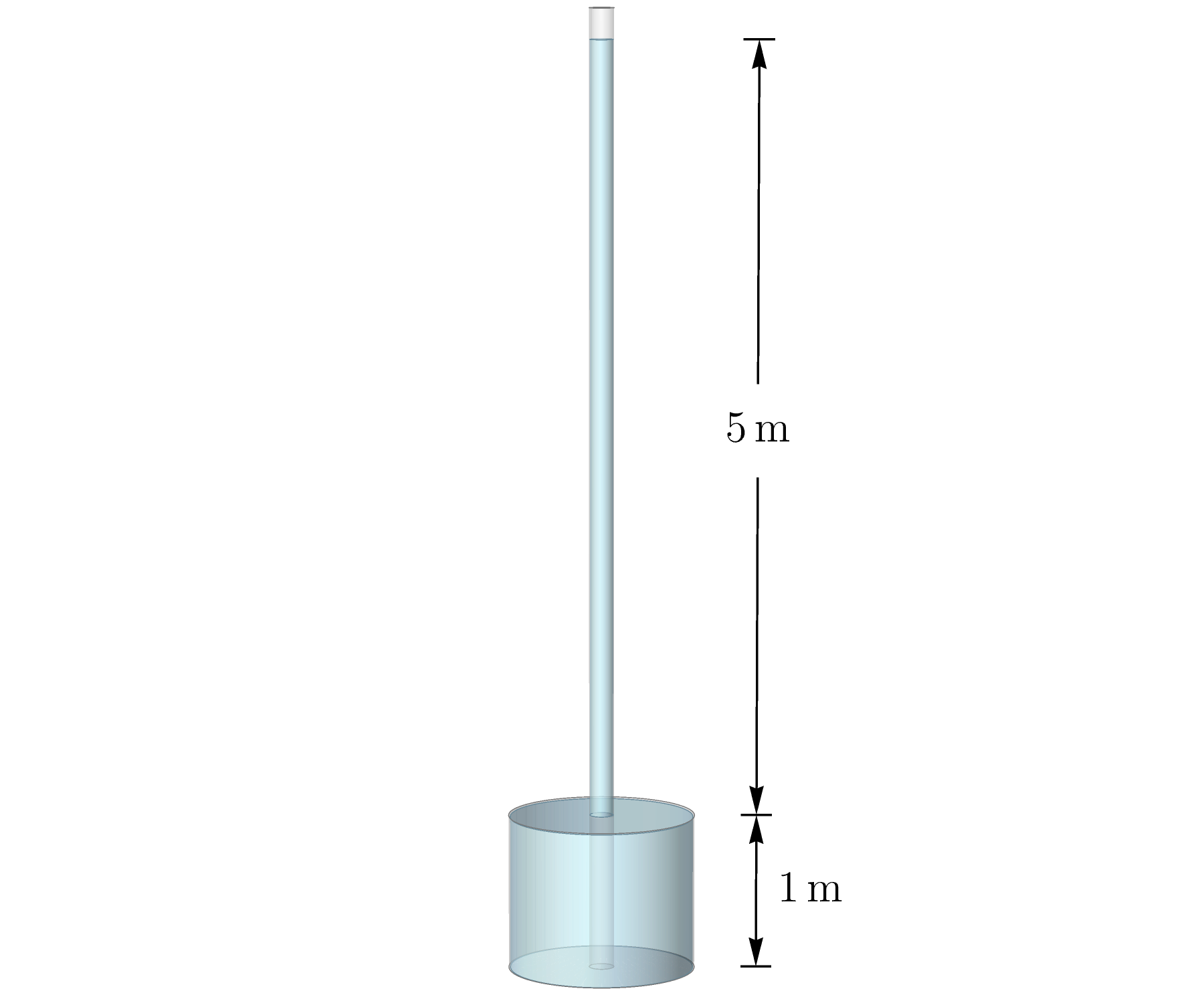
Figure Q13.38
Explanation
Water has a mass density of $1000\,\text{kg}/\text{m}^3$. In terms of weight, the density of water is expressed as \begin{align} \text{Weight density} &= \text{mass density}\times g \nonumber\\[6pt] &= 1000\,\text{kg}/\text{m}^3\times 10\,\text{m}/\text{s}^2 \nonumber\\[6pt] &= 10{,}000\,\text{N}/\text{m}^3 \nonumber\\[6pt] &= 10\,\text{kN}/\text{m}^3 \end{align} For the barrel filled with water, you can calculate the pressure near the bottom (at 1 m depth) as \begin{align} \text{Water pressure}\, (1\,\text{m}) &= \text{weight density} \times \text{depth} \nonumber\\[6pt] &= 10\,\text{kN}/\text{m}^3 \times 1\,\text{m} \nonumber\\[6pt] &= 10\,\text{kN}/\text{m}^2 \nonumber\\[6pt] &= 10\,\text{kPa} \end{align} When the thin pipe extending from the barrel is filled with water (see Figure Q13.38), the pressure at the bottom of the barrel increases: \begin{align} \text{Water pressure}\, (6\,\text{m}) &= \text{weight density} \times \text{depth} \nonumber\\[6pt] &= 10\,\text{kN}/\text{m}^3 \times (5\,\text{m} + 1\,\text{m}) \nonumber\\[6pt] &= 10\,\text{kN}/\text{m}^3 \times 6\,\text{m} \nonumber\\[6pt] &= 60\,\text{kPa} \end{align} Since liquid pressure depends on vertical location only, all points at the bottom of the barrel experience a pressure of 60 kPa.
Chapter 13
Question 44
In the hydraulic pistons shown in the sketch, the small piston has a diameter of 2 cm. The large piston has a diameter of 6 cm. How much more force can the larger piston exert compared with the force applied to the smaller piston?
Figure Q13.44(a)
Answer
Nine times the force.
Diagram
Figure Q13.44(b)
Explanation
When comparing the area of the larger piston (radius 3 cm) with that of the smaller piston (radius 1 cm), you obtain the following ratio: \begin{align} \frac{\text{Area of larger piston}}{\text{Area of smaller piston}} &= \frac{\pi\, (3\,\text{cm})^2}{\pi\, (1\,\text{cm})^2} \nonumber\\[6pt] &= \frac{9}{1} \nonumber\\[6pt] &= 9 \end{align} Since the area of the larger piston is nine times the area of the smaller piston, a 1-N input force applied to the smaller piston results in an output force of 9 N exerted by the larger piston.
Chapter 13
Question 45
Rank the bottom pressures from most to least for the following:
- A 20-cm-tall container of saltwater
- A 20-cm-tall container of freshwater
- A 10-cm-tall container of mercury
Answer
c, a, b
Explanation
The pressure at a certain depth below the surface of a liquid is calculated using the formula \begin{equation} \text{Liquid pressure} = \text{weight density} \times \text{depth} \end{equation} where the weight density refers to the weight per unit volume of the liquid. Table 12.1 in the eText gives the density (i.e., mass per unit volume) for each of the three liquids. The corresponding weight densities are \begin{align} 1025\,\text{kg}/\text{m}^3 \times g &= 10{,}250\,\text{N}/\text{m}^3 \quad \text{for saltwater} \nonumber\\[6pt] 1000\,\text{kg}/\text{m}^3 \times g &= 10{,}000\,\text{N}/\text{m}^3 \quad\text{for freshwater}\nonumber\\[6pt] 13{,}600\,\text{kg}/\text{m}^3 \times g &= 136{,}000\,\text{N}/\text{m}^3 \quad\text{for mercury} \\[6pt] \end{align} where the acceleration due to gravity $g = 10\,\text{m}/\text{s}^2$.
- At a 20-cm depth in saltwater, \begin{align} \text{Liquid pressure} &= 10{,}250\,\text{N}/\text{m}^3 \times 0.2\,\text{m} \nonumber\\[6pt] &= 2050\,\text{N}/\text{m}^2 \end{align}
- At a 20-cm depth in freshwater, \begin{align} \text{Liquid pressure} &= 10{,}000\,\text{N}/\text{m}^3 \times 0.2\,\text{m} \nonumber\\[6pt] &= 2000\,\text{N}/\text{m}^2 \end{align}
- At a 10-cm depth in mercury, \begin{align} \text{Liquid pressure} &= 136{,}000\,\text{N}/\text{m}^3 \times 0.1\,\text{m} \nonumber\\[6pt] &= 13{,}600\,\text{N}/\text{m}^2 \end{align}
Chapter 13
Question 58
A block of aluminum with a volume of 10 cm3 is placed in a beaker of water filled to the brim. Water overflows. The same is done in another beaker with a 10-cm3 block of lead. Does the lead displace more, less, or the same amount of water as the aluminum does?
Answer
The block of lead displaces the same amount of water as the block of aluminum of equal volume.
Explanation
Aluminum and lead have densities greater than that of water (see Table 12.1 in the eText). Therefore, each block sinks to the bottom of the beaker and becomes entirely submerged. Since both blocks have the same volume, they displace equal amounts of water (10 cm3).
Chapter 13
Question 59
A block of aluminum with a mass of 1 kg is placed in a beaker of water filled to the brim. Water overflows. The same is done in another beaker with a 1-kg block of lead. Does the lead displace more, less, or the same amount of water as the aluminum does?
Answer
The block of lead displaces less water than the block of aluminum of equal mass.
Explanation
In Table 12.1 in the eText, you see the density of lead is approximately four times the density of aluminum. Therefore, an aluminum block is four times larger in size (or volume) than a block of lead of equal mass.
Note that the volume of a 1-kg block of lead is calculated as follows: \begin{align} \text{Volume of lead block} &= \frac{\text{mass}}{\text{density}} \nonumber\\[6pt] &= \frac{1\,\text{kg}}{11{,}340\,\text{kg}/\text{m}^3} \nonumber\\[6pt] &= \frac{1000\,\text{g}}{11.34\,\text{g}/\text{cm}^3} \nonumber\\[6pt] &= 88\,\text{cm}^3 \end{align} For a 1-kg block of aluminum, \begin{align} \text{Volume of aluminum block} &= \frac{1000\,\text{g}}{2.7\,\text{g}/\text{cm}^3} \nonumber\\[6pt] &= 370\,\text{cm}^3 \end{align}
Chapter 13
Question 67
A can of diet soda floats in water, whereas a can of regular soda sinks. Explain this phenomenon first in terms of density, then in terms of weight versus buoyant force.
Hint
Consider the effect of the sugar content in the regular soda.
Answer
Regular soda is denser than water due to its sugar content. A can of regular soda normally has 39 g of sugar dissolved in it, causing the density of the soda to be greater than that of pure water. Therefore, the can sinks in water.
To make diet soda, a relatively tiny amount of sweetener (e.g., aspartame) is dissolved in the liquid, which ends up being slightly less dense than water. Therefore, the can of diet soda floats on water.
You can also say that a can of regular soda sinks because its weight is slightly greater than the buoyant force, while the weight of a can of diet soda is slightly less than the buoyant force.
Chapter 13
Question 71
How much force is needed to hold a nearly weightless but rigid 1-L carton beneath the water surface?
Answer
10 N
Explanation
The buoyant force exerted on a 1-L carton submerged under water is equal to the weight of the displaced water. Since 1 L of water has a mass of 1 kg, you can write \begin{align} \text{Buoyant force} &= \text{weight of displaced water} \nonumber\\[6pt] &= 1\,\text{kg}\times 10\,\text{m}/\text{s}^2 \nonumber\\[6pt] &= 10\,\text{N} \end{align} Given that the carton has negligible weight, you will need to push down with a $10$-$\text{N}$ force to hold the carton beneath the water surface.
Chapter 13
Question 72
Why will a volleyball held beneath the water surface have more buoyant force than if it is floating?
Answer
The weight of the displaced water is greater for the submerged ball.
Explanation
The buoyant force that pushes upward on an object is equal to the weight of the displaced water. A volleyball held beneath the surface displaces more water than if it is floating on the surface (or partially submerged).
Chapter 13
Question 79
A ship sailing from the ocean into a freshwater harbor sinks slightly deeper into the water. Does the buoyant force on the ship change? If so, does it increase or decrease?
Answer
The buoyant force remains the same.
Explanation
The buoyant force required to keep the ship floating is equal to its weight. The buoyant force is also equal to the weight of displaced water. Since freshwater is slightly less dense than seawater, the ship sinks slightly deeper, displacing more freshwater and maintaining the same buoyant force.
Chapter 13
Question 87
A small aquarium half-filled with water is on a spring scale. Will the reading of the scale increase or remain the same if a fish is placed in the aquarium? (Will your answer be different if the aquarium is initially filled to the brim?)
Answer
The weight of the half-filled aquarium increases when a fish is placed inside but remains unchanged if the aquarium is initially filled to the brim.
Explanation
When the aquarium is half-filled with water, the added fish causes the reading of the scale to increase by an amount equal to the weight of the fish. Note that the amount of water in the aquarium does not change in this case.
The reading of the scale remains unchanged if the fish is placed in the aquarium when it is filled with water to the brim. This is because the density of the fish is equal to that of water and, therefore, the weight of the water that spills over the brim is equal to the weight of the fish.
Chapter 13
Question 92
In the hydraulic arrangement shown, the larger piston has an area that is 50 times that of the smaller piston. The strong man hopes to exert enough force on the large piston to raise the 10 kg that rest on the small piston. Do you think he will be successful? Defend your answer.
Figure Q13.92
Answer
He will not be successful.
Explanation
Since the area of the larger piston is 50 times that of the smaller piston, the strong man needs to exert a force that is at least 50 times the weight of the 10-kg object. This is impossible in the arrangement shown because the strong man cannot apply a downward force on the piston of more than his weight, which is less than 500 kg.
Normally, a hydraulic system is arranged so the input force is applied against the smaller piston and the output force is exerted by the wider piston. The arrangement in this question is reversed.
Chapter 13
Question 94
Why will hot water flow more readily than cold water through small leaks in a car radiator?
Answer
Hot water has less surface tension.
Explanation
The molecules in hot water move more rapidly and do not adhere to one another as well as the molecules in cold water. As a result, hot water has lower surface tension and leaks more easily through thin cracks and small openings in a radiator.
Chapter 13
Question 106
A piece of iron placed on a block of wood makes it float lower in the water. If the iron were instead suspended beneath the wood, would the wood float as low, lower, or higher than when the iron is on top? Discuss.
Answer
The wood would float higher.
Diagram
Figure Q13.106
Explanation
Since the block of wood and the piece of iron have the same weight in both situations, equal amounts of water are displaced to support their combined weight. As shown in Figure Q13.106, when the piece of iron is placed on top of the wood block, water is displaced by only the submerged portion of the block. However, when the piece of iron is suspended underneath the wood, the submerged iron displaces an amount of water equal to its volume, leaving less water to be displaced by the wood block.
Chapter 13
Question 111
Would the water level in a canal lock go up or down if a battleship in the lock sank? Discuss your answer.
Answer
The water level would go down.
Explanation
The amount of water displaced by a floating ship is equal to its weight. However, if a battleship sinks, the water displaced has the same volume as the material (predominantly steel) that makes up the ship. Since the density of steel is eight times that of water, the weight of the displaced water is one-eighth the weight of the submerged battleship.
Chapter 13
Question 117
If the gravitational field of Earth were to increase, would a fish float to the surface, sink, or stay at the same depth?
Answer
Stay at the same depth.
Explanation
If the gravitational field of Earth were to increase (i.e., $g$ becomes larger), the weight of the fish would increase. However, the weight density of water and the water pressure would also increase by equal factors. Therefore, the fish would remain at the same depth.
Exercises
Spend some time completing the following exercises to test your understanding of the main concepts in Chapter 13 and increase your efficiency in answering exam questions.
End-of-Chapter Practice Questions
Answer questions 5, 7, 13, 15, 21, 23, 33, 35, 37, 41, 43, 49, 55, 57, 65, 77, 83, 89, 95, 97, 103, and 107 from Chapter 13 of the eText. If you require assistance, please contact your tutor. The answers are provided at the end of the eText.