Unit 8: Rotational Motion
Keeping a bike stable is easy while you are moving. However, when you stop, you must hold the bike or use the kickstand to prevent it from toppling. After completing this unit, you should be able to use the law of conservation of angular momentum to explain this observation.
Learning Outcomes
By the end of this unit, you should be able to
- give examples of circular motion.
- explain rotational inertia and compare it with mass.
- define torque and demonstrate how the same force can produce different torques.
- define center of mass and center of gravity and discuss the conditions of stability.
- describe centripetal and centrifugal forces and explain how gravity can be simulated in rotating reference frames.
- define angular momentum and explain how it is related to linear momentum.
- state the law of conservation of angular momentum and give examples of its applications.
eText Material
Reading Assignment
Read the following sections in Chapter 8 of the eText:
- 8.1: Circular Motion
- 8.2: Centripetal Force
- 8.3: Centrifugal Force
- 8.4: Rotational Inertia
- 8.5: Torque
- 8.6: Center of Mass and Center of Gravity
- 8.7: Angular Momentum
- 8.8: Conservation of Angular Momentum
Supplementary learning resources are available on the Mastering Physics learning platform.
Additional Reading
Circular Motion
When you study circular motion, it is simpler to work with angles rather than distances. In Figure 8.1, a small object rotates about a fixed axis and sweeps out an angle $\Delta\theta$ during a time interval $\Delta t$. The object traces a circular arc of length $\Delta s$ and radius $r$ during the same period. The relationship between the angular shift $\Delta\theta$ and the corresponding linear distance $\Delta s$ along the circular path is given by
\begin{equation} \Delta\theta = \frac{\Delta s}{r} \label{unit08_dth_ds_dr} \end{equation}
Here, the unit of $\Delta\theta$ is radians (denoted by rad).
Figure 8.1: An object in uniform circular motion.
In a full revolution (rev), the object travels a distance equal to the circumference ($2\pi r$) of the circular path. The angle swept out by the object in this case is $2\pi\,\text{rad}$. Note that \begin{equation} 1\,\text{rev} = 2\pi\,\text{rad} = 360^\circ \end{equation}
Rotational Speed
The linear or tangential speed of the object in Figure 8.1 is given by \begin{equation} v = \frac{\Delta s}{\Delta t} \end{equation} Note that the velocity vector continuously changes direction, as it is always tangent to the circular path. The rotational speed of the object as it rotates an angle $\Delta\theta$ during a time interval $\Delta t$ is defined as
\begin{equation} \omega = \frac{\Delta\theta}{\Delta t} \label{unit08_domega_dth_dt} \end{equation}
The units commonly used for rotational speed include radians per second (rad/s) and revolutions per minute (RPM).
Substituting from Equation 8.1 into Equation 8.4, you have \begin{align} \omega &= \frac{\left(\Delta s/r\right)}{\Delta t} \nonumber\\[6pt] &= \frac{\left(\Delta s/\Delta t\right)}{r} \nonumber\\[6pt] &= \frac{v}{r} \end{align} or \begin{equation} v = \omega\, r \end{equation}
Torque
Consider a small object of mass $m$ that is restricted to move along a circular path of radius $r$. Suppose a force $F$ acts on the object parallel to its direction of motion, as shown in Figure 8.2. According to Newton’s second law of motion, the linear acceleration of the object is proportional to the net external force (or $F = ma$). Is there a similar relationship for rotational motion? The answer is yes:
The rotational acceleration of a rotating object is proportional to the net external torque.
Figure 8.2: An object rotates along a circular path under the influence of a constant force.
Torque ($\tau$) is a physical quantity equal to the applied force multiplied by the lever arm (i.e., the perpendicular distance between the applied force and the axis of rotation). So the object in Figure 8.2 experiences a torque about the axis of rotation $O$, as given below:
\begin{align} \text{Torque} &= \text{lever arm} \times \text{force} \nonumber\\[6pt] \Rightarrow\quad \tau &= r F \nonumber\\[6pt] &= r\, (m a) \nonumber\\[6pt] &= (m r^2)\,\alpha \label{unit08_tau_rf} \end{align}
In Equation 8.7, $a$ is the linear acceleration tangent to the circular arc and
\begin{equation} \alpha = \frac{a}{r} \end{equation}
is the corresponding rotational acceleration. The quantity between brackets is called the rotational inertia ($I$) and, in this case, is given as
\begin{equation} I = m r^2 \label{unit08_Iparticle} \end{equation}
Note that Equation 8.9 is applicable to a particle (or small object) of mass $m$ rotating along a circular path of radius $r$.
Equation 8.7 can be expressed in the more general form of \begin{equation} \tau = I \alpha \label{unit08_tau_Ialpha} \end{equation} In the absence of a net torque (i.e., $\tau = 0$), rotational acceleration is equal to zero and the object rotates at a constant rotational speed. When a net constant torque is applied, the object experiences constant rotational acceleration.
The similarity between the relations $\tau = I\alpha$ and $F = ma$ requires further exploration. Torque $\tau$ plays a similar role in rotational motion as $F$ does in linear motion, where the rotational acceleration $\alpha$ corresponds to the linear acceleration $a$ and the moment of inertia $I$ is the rotational equivalent of the mass $m$. Note, however, that the moment of inertia is not a simple intrinsic quantity and can have different values for the same object, depending on the object’s geometry and the location of the pivot axis.
Center of Mass
In studying the motion of various objects, we have been treating the objects as point masses without explicitly saying so. In real life, you deal with three-dimensional extended objects, which may create a problem in specifying locations. In other words, what point inside (or outside) the object do you use to mark its exact position? Another added complication is that a three-dimensional object may rotate or spin while in motion, causing different parts of the object to have different velocities.
For a given object, however, you can imagine that the total mass of the object is concentrated at a specific point, called the center of mass. The motion of an object can then be analyzed into a translational motion (of the center of mass) and a rotational motion about the center of mass. In other words, the exercises you have done so far where you treated extended objects as point masses were not meaningless exercises. You just need to consider rotation as well.
When the mass of the object is evenly distributed over its entire volume, the center of mass coincides with the geometric center of the object. For example, the center of mass of a uniform solid sphere is at the center of the sphere. The center of mass of a ball (a hollow sphere) of uniform thickness is at the center of the ball. However, for the L-shaped object shown in Figure 8.3, the center of mass is located outside the object.
Figure 8.3: Centers of mass of two objects.
Another related term is the center of gravity, which refers to the point at which the force of gravity appears to act. The center of gravity of an extended object may differ from its center of mass if the gravitational acceleration cannot be assumed to be uniform throughout the object. However, for the purposes of this course, the terms center of mass and center of gravity are used interchangeably.
Simulation
Run the Balancing Act simulation to play with objects on a seesaw to learn about balancing torques.
Simulation by PhET Interactive Simulations, University of Colorado Boulder, licensed under CC-BY-4.0 (https://phet.colorado.edu)
Centripetal Force
An object accelerates if its speed or the direction of motion changes. According to Newton’s second law of motion, a force is required to generate such acceleration. A force applied parallel to the velocity of an object changes its speed without affecting the direction of motion. If, however, the applied force is perpendicular to the direction of motion, the object turns while maintaining the same speed. In all other situations, both the speed and the direction of motion will change.
Figure 8.4: Centripetal force on an object in uniform circular motion.
The motion of an object traveling at a constant speed along a circular path is called uniform circular motion. Even though the speed is constant, the direction of motion continuously changes with time. As shown in Figure 8.4, the applied force always acts perpendicular to the direction of motion, toward the center of the circular path. This force is referred to as centripetal force ($F_c$), and its value is given by \begin{equation} F_c = \frac{m v^2}{r} = m\, \omega^2\, r \label{unit08_ac_v2r} \end{equation}
Centrifugal Force
When you tie a rock or some other object to the end of a string and swing it around, you feel a pull on your fingers. The faster you rotate the rock, the stronger the pull. You may have heard of the concept of centrifugal force, which supposedly pulls outward on the center of an object in circular motion. Actually, the rock at the end of the string does not experience an outward-pulling force; the only force acting upon it (other than gravity) is centripetal force.
So what happens when you let go of the string? The moment you do so, the source of the centripetal force, which is the tension in the string, becomes nonexistent. Since the force deflecting the motion disappears, the rock continues to move in a direction tangent to the circle at the point of release.
Angular Momentum
Consider a particle of a mass $m$ that moves at a speed $v$. You can describe the motion of the particle by its linear momentum ($mv$). Angular momentum, a related quantity, is defined in association with a specific axis of rotation through the origin: \begin{align} \text{Angular momentum} &= \text{rotational inertia} \times \text{rotational speed} \nonumber\\[6pt] &= I \omega\ \nonumber\\[6pt] &= (m r^2) \left(\frac{v}{r}\right) \nonumber\\[6pt] &= m v r \label{unit08_Lrp} \end{align} In the absence of any external torque, the net angular momentum of a system remains constant.
Questions
The following questions are selected from the end of Chapter 8 of the eText. It is important to your learning that you try to answer each question independently before you read through the answer and explanation given.
For questions that ask you to explain or discuss your answer, the response revealed by the Answer button would earn you only partial marks on a quiz or exam in this course. Use the Answer to help you formulate a complete answer before you select the Explanation button to check your work.
Note that some questions have been adapted to suit the format of this course.
Chapter 8
Question 13
As distance increases between most of the mass of an object and its center of rotation, does rotational inertia increase or decrease?
Answer
It increases.
Diagram
Figure Q8.13
Explanation
The rod in Figure Q8.13 is an example of an object whose rotational inertia differs depending on the rotational axis. Note that when the axis of rotation shifts from the center of the rod to one of its ends, the rotational inertia increases by four times.
Chapter 8
Question 18
How do clockwise and counterclockwise torques compare when a system is balanced?
Answer
The torques are equal in magnitude.
Explanation
A clockwise torque tends to turn a system in the clockwise direction, while a counterclockwise torque does the opposite. A balanced system is in a state of mechanical equilibrium and experiences a net torque equal to zero. Therefore, the two opposing torques on the system must have the same magnitude.
Chapter 8
Question 49
To tighten a bolt, you push with a force of 80 N at the end of a wrench handle that is 0.25 m from the axis of the bolt.
- What torque are you exerting?
- Show that if you move your hand inward to be only 0.10 m from the bolt, you should exert 200 N of force to achieve the same torque.
- Do your answers depend on the direction of your push relative to the direction of the wrench handle?
Answer
- $20\,\text{N}\cdot\text{m}$
- 200 N
- Yes.
Explanation
Assume the force is exerted perpendicular to the wrench handle. When you push with a force of 80 N at a distance of 0.25 m from the axis of the bolt, you exert a torque given as \begin{align} \text{Torque} &= \text{lever arm} \times \text{force} \nonumber\\[6pt] &= 0.25\,\text{m} \times 80\,\text{N} \nonumber\\[6pt] &= 20\,\text{N}\cdot\text{m} \end{align}
When you reduce the lever arm to 0.10 m, you achieve the same torque by exerting a force $F$ calculated as follows: \begin{align} 20\,\text{N}\cdot\text{m} &= 0.10\,\text{m} \times F \nonumber\\[6pt] \Rightarrow\quad F &= \frac{20\,\text{N}\cdot\text{m}}{0.10\,\text{m}} \nonumber\\[6pt] &= 200\,\text{N} \end{align} You maximize the force applied to the lever arm when you direct it perpendicular to the handle. Therefore, the torque applied on the bolt depends on the direction of your push relative to the direction of the wrench handle.
Chapter 8
Question 50
The rock and meterstick balance at the 25-cm mark, as shown. The meterstick has a mass of 1 kg. What must be the mass of the rock?
Figure Q8.50(a)
Answer
1 kg
Diagram
Figure Q8.50(b)
Explanation
The mass of the 1-kg meterstick is divided into 0.25 kg for the shorter section and 0.75 kg for the longer section. To ensure equilibrium, the net torque about the 25-cm mark must be equal to zero. As shown in Figure Q8.50(b), equilibrium is achieved when the counterclockwise torque produced by the combined weight of the rock and the shorter section of the meterstick is balanced by the clockwise torque produced by the weight of the longer section.
The weight of the longer section of the meterstick is equal to 7.5 N and is represented by a downward arrow at its center of mass (i.e., 37.5 cm to the right of the fulcrum). So the clockwise torque on the system is given as
\begin{align} \text{Clockwise torque} &= 7.5\,\text{N} \times 0.375\,\text{m} \nonumber\\[6pt] &= 2.8125\,\text{N}\cdot\text{m} \label{ch08_q46_clockwise} \end{align}
Similarly, the shorter section of the meterstick has a weight of 2.5 N, which acts 12.5 cm to the left of the fulcrum. If $mg$ is the rock’s weight, the net counterclockwise torque on the system is given by
\begin{align} \text{Counterclockwise torque} &= (mg \times 0.25\,\text{m}) + (2.5\,\text{N} \times 0.125\,\text{m}) \nonumber\\[6pt] &= (mg \times 0.25\,\text{m}) + 0.3125\,\text{N}\cdot\text{m} \label{ch08_q46_counterclockwise} \end{align}
Since the system is balanced, Equations 8.15 and 8.16 are equal and you can write \begin{align} (mg \times 0.25\,\text{m}) + 0.3125\,\text{N}\cdot\text{m} &= 2.8125\,\text{N}\cdot\text{m} \nonumber\\[6pt] \Rightarrow\quad mg \times 0.25\,\text{m} &= 2.5\,\text{N}\cdot\text{m} \nonumber\\[6pt] \Rightarrow\quad mg &= 10\,\text{N} \end{align} You can then calculate the mass of the rock: \begin{align} m &= \frac{10\,\text{N}}{g} \nonumber\\[6pt] &= \frac{10\,\text{N}}{10\,\text{m}/\text{s}^2} \nonumber\\[6pt] &= 1\,\text{kg} \end{align}
Chapter 8
Question 51
An ice puck of mass $m$ revolves on an icy surface in a circle at speed $v$ at the end of a horizontal string of length $\ell$. The tension in the string is $T$.
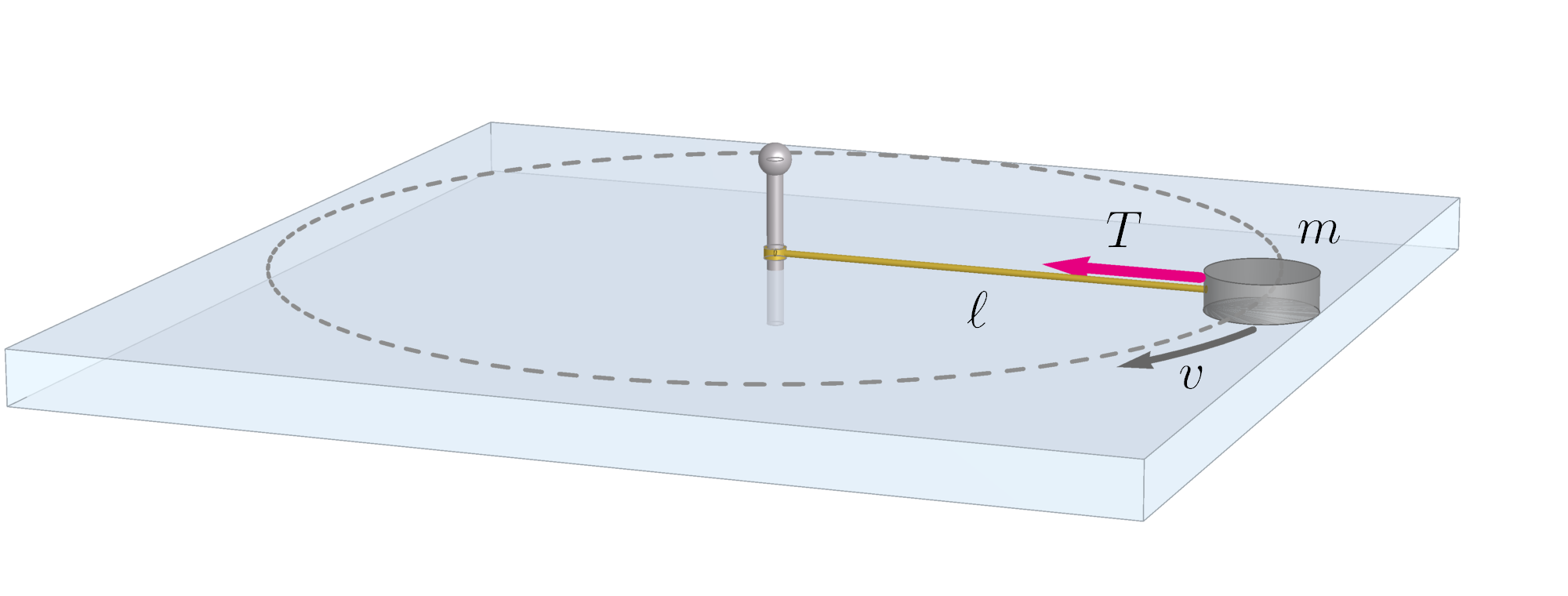
Figure Q8.51
- Substitute the values $T$ and $\ell$ in the equation for centripetal force.
- Rearrange the equation to solve for mass.
- Show that the mass of the puck is 5 kg when the length of the string is 2 m, the string tension is 10 N, and the tangential speed of the puck is 2 m/s.
Answer
- $T = \dfrac{m v^2}{\ell}$
- $m = \dfrac{\ell T}{v^2}$
- $m = \dfrac{2\,\text{m} \times 10\,\text{N}}{(2\,\text{m/s})^2} = 5\,\text{kg}$
Explanation
- The centripetal force here is provided by the tension $T$ in the string, which causes the puck to rotate in a circular path of radius $\ell$. So the relevant equation in this case is expressed as \begin{equation} T = \frac{m v^2}{\ell} \end{equation}
When multiplying both sides of the equation above by $\ell$ and dividing by $v^2$, you can write
\begin{align} \frac{\ell}{v^2} \times T &= \frac{\ell}{v^2} \times \frac{m v^2}{\ell} \nonumber\\[6pt] \Rightarrow\quad m &= \frac{\ell T}{v^2} \label{ch08_q51_m} \end{align}
- You calculate the mass of the puck by substituting $\ell = 2\,\text{m}$, $T = 10\,\text{N}$, and $v = 2\,\text{m/s}$ into Equation 8.20: \begin{align} m &= \frac{(2\,\text{m}) (10\,\text{N})}{(2\,\text{m/s})^2} \nonumber\\[6pt] &= 5\,\text{kg} \end{align}
Chapter 8
Question 52
If a trapeze artist rotates once each second while sailing through the air and contracts to reduce her rotational inertia to one-third of what it was, how many rotations per second will result?
Answer
Three rotations per second.
Explanation
Neglecting the external torque due to air resistance, the angular momentum ($I \omega$) of the trapeze artist is conserved. Since, her rotational inertia ($I$) reduces to one-third its initial value, the angular velocity ($\omega$) must triple in order to keep the angular momentum constant. Mathematically, this can be expressed as \begin{equation} I \omega = \dfrac{1}{3}\, I\times 3\, \omega \end{equation}
Chapter 8
Question 56
Beginning from a rest position, a solid disk A, a solid ball B, and a hoop C race down an inclined plane. Rank them in reaching the bottom: winner, second place, and third place.
Figure Q8.56
Answer
B is the winner, A comes in second place, and C comes in third place.
Explanation
A round object with greater rotational inertia has more resistance to changing its rotational speed than a round object with less rotational inertia. Referring to Table 8.1 in the eText, you see that the rotational inertia per unit mass for the three objects in the race is given by \begin{align} \frac{I}{m} &= r^2 \quad (\text{hoop}) \\[6pt] \frac{I}{m} &= \dfrac{1}{2} r^2 = 0.5\, r^2 \quad (\text{solid disk}) \\[6pt] \frac{I}{m} &= \dfrac{2}{5} r^2 = 0.4\, r^2 \quad (\text{solid ball}) \end{align} Therefore, the solid ball in Figure Q8.56 has the greatest acceleration, followed by the solid disk and then the hoop.
Chapter 8
Question 64
Use the relationship $v \sim r \omega$ to explain why the end of a flyswatter moves much faster than your hand gripping the flyswatter when swatting a fly.
Hint
Note that the end of the flyswatter moves over a larger arc than your hand does during the same time interval.
Diagram
Figure Q8.64
Answer
As shown in Figure Q8.64, your hand and the flyswatter are lined up and rotate with the same rotational speed ($\omega$) with respect to the wrist joint. Therefore, the linear speed ($v$) depends on the radius of rotation ($r$) and is given by \begin{equation} v = r \omega \end{equation} Since the radius of rotation of the flyswatter is greater than the radius of rotation of your hand, the flyswatter moves faster.
Chapter 8
Question 71
Discuss how a roll down an incline would help distinguish between two identical-looking spheres of the same weight, one solid and the other hollow.
Hint
Note that the solid sphere has less rotational inertia compared with the hollow sphere.
Answer
You would release the two spheres from rest at the top of the incline to see which one reaches the bottom first. The entire mass of the hollow sphere is concentrated near its surface, while the mass of the solid sphere is distributed uniformly inside it. As a result, the solid sphere has less rotational inertia and, therefore, would roll down the incline with greater acceleration than the hollow sphere.
Chapter 8
Question 74
In terms of a torque’s lever arm, why is a doorknob placed far from the hinges?
Answer
To maximize the torque produced when you push or pull the knob.
Explanation
Torque is equal to the applied force times the length of the lever arm (or $\tau = F r$). When there is no lever arm ($r = 0$), the torque ($\tau$) is equal to zero. For example, if you push a door at the edge where the hinges are attached, the door experiences zero torque and no rotation is achieved.
Chapter 8
Question 77
When a bowling ball leaves your hand, it may not spin. But farther along the lane, it does spin. What produces the spinning?
Answer
Friction with the floor.
Diagram
Figure Q8.77
Explanation
After you throw the bowling ball down the lane, the nonspinning ball experiences a frictional force with the floor, which acts on the ball in the backward direction (see Figure Q8.77). The resulting nonzero torque causes the ball to spin about its center and roll forward.
Chapter 8
Question 88
The centers of gravity of the three trucks parked on a hill are shown by the Xs. Which truck(s) will tip over? Defend your answer.
Figure Q8.88(a)
Answer
The first truck on the left.
Diagram
Figure Q8.88(b)
Explanation
Start by drawing a vertical arrow through the center of mass of each truck (see Figure Q8.88(b)) to represent the downward force of gravity. The truck tips over when its weight generates a counterclockwise torque about an axis through the left set of wheels.
In Figure Q8.88(b), you see that the weight arrow for the middle truck passes through a point on the ground located between the truck’s left and right wheels. This is also the case for the truck on the right. As a result, these two trucks should be stable. The truck on the left, however, experiences a net torque in the counterclockwise direction, which will cause it to rotate about its left set of wheels and tip over.
Chapter 8
Question 89
A racing car on a flat circular track needs friction between the tires and the track to maintain its circular motion. How much more friction is required for twice the speed? Explain how you arrive at your answer.
Answer
Four times more friction.
Explanation
The centripetal force required to keep an object of mass $m$ moving with a speed $v$ along a circular path of radius $r$ is given by the equation \begin{equation} F = \frac{m v^2}{r} \end{equation} For twice the speed, the new centripetal force required to keep the car on the track is given by \begin{align} F^\prime &= \frac{m\, (2v)^2}{r} \nonumber\\[6pt] &= 4 \left(\frac{m v^2}{r}\right) \nonumber\\[6pt] &= 4 F \nonumber\\[6pt] \end{align} So when the speed of the car doubles, the required force of friction quadruples.
Chapter 8
Question 94
The sketch shows a coin at the edge of a turntable. The weight of the coin is shown by the vector $\bf w$. Two other forces act on the coin—the normal force and a force of friction that prevents it from sliding off the edge. Draw force vectors for both of these.
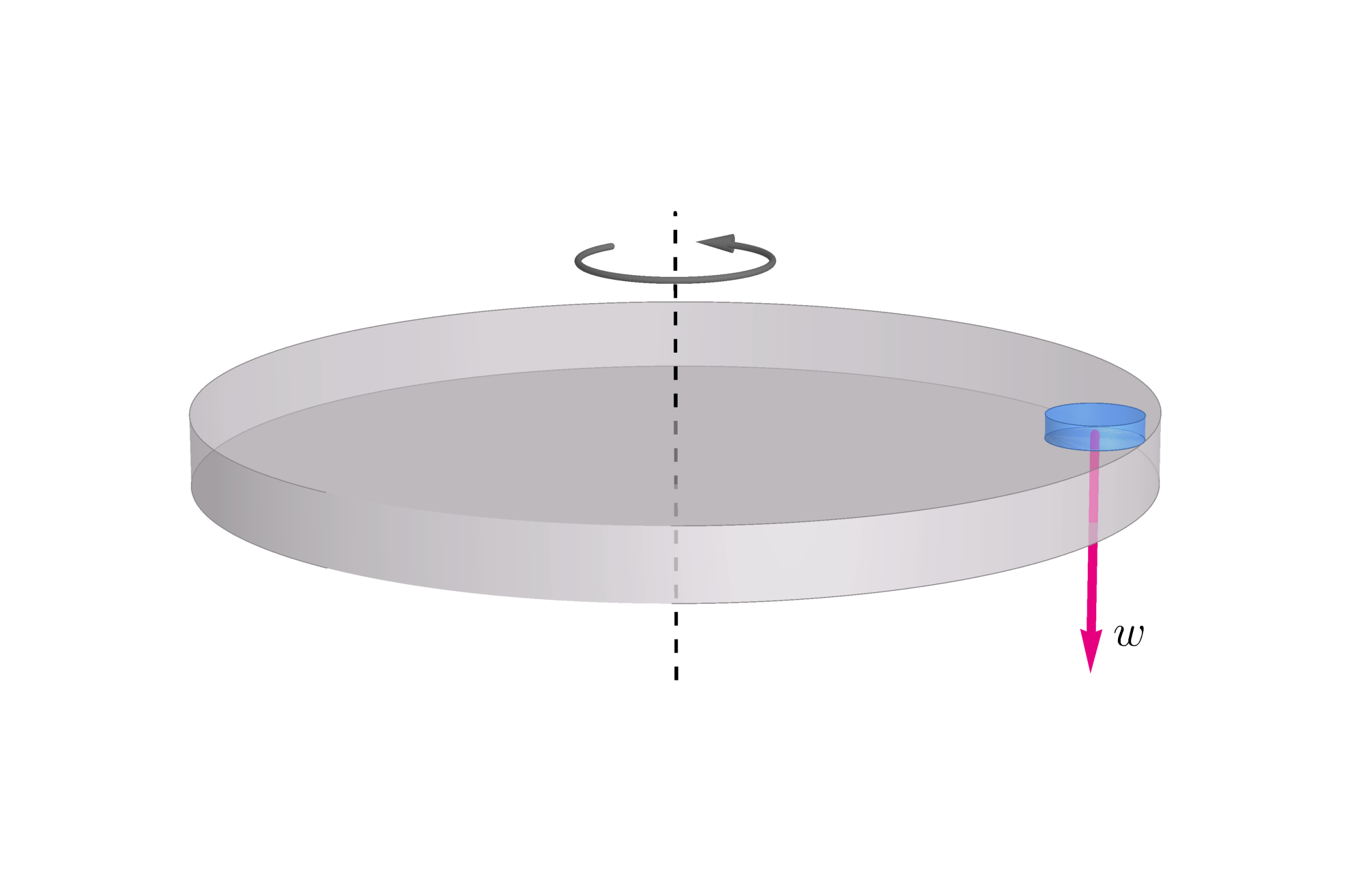
Figure Q8.94(a)
Diagram
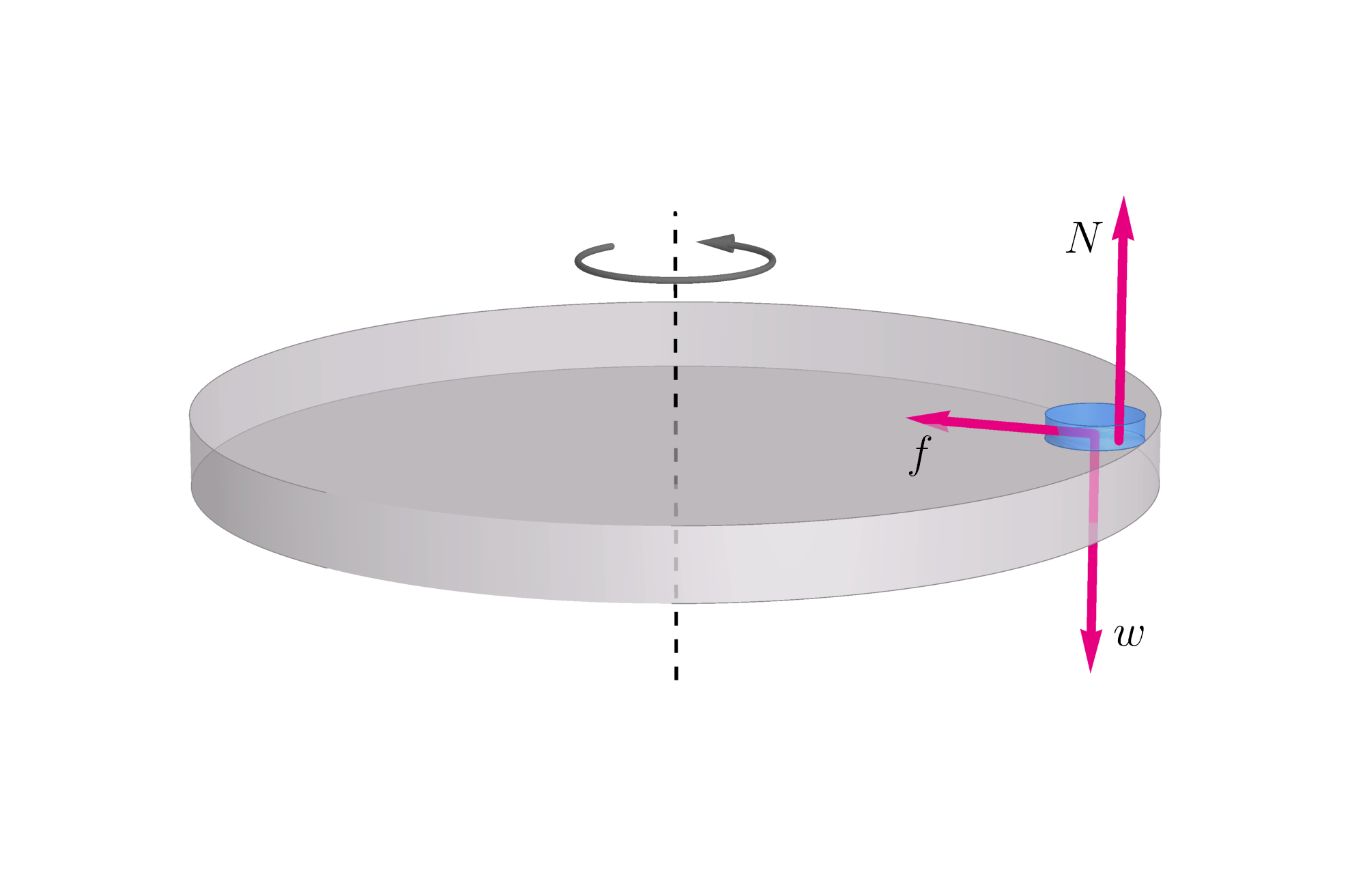
Figure Q8.94(b)
Answer
Gravitational attraction exerts a downward force on the coin equal to its weight ($w = mg$). As shown in Figure Q8.94(b), the tabletop exerts an equal upward force, called the normal force ($N = w$), which prevents the coin from falling through the table. The force of friction ($f$) acts parallel to the surface of the table, toward the axis of rotation, and provides the necessary centripetal force to maintain the coin’s rotation and prevent it from sliding off the edge.
Chapter 8
Question 99
You sit at the middle of a large turntable at an amusement park as it is set spinning and then allowed to spin freely. When you crawl toward the edge of the turntable, does the rate of the rotation increase, decrease, or remain unchanged? What physics principle supports your answer?
Answer
The rate of rotation decreases, as given by the law of conservation of angular momentum.
Explanation
The angular momentum of the rotating system is equal to its rotational inertia ($I$) multiplied by its rotational velocity ($\omega$). As you crawl away from the center of the turntable, you increase your radius of rotation and the rotational inertia of the system (the turntable and you) becomes larger. Since no external torques are involved, the angular momentum of the system remains unchanged: \begin{align} \text{Initial angular momentum} &= \text{final angular momentum} \nonumber\\[6pt] \Rightarrow\quad (I\,\omega)_\text{before} &= (I\,\omega)_\text{after} \end{align} From the equation above, you see that if $I$ increases, $\omega$ must decrease by an equal factor for $I\omega$ to remain constant. Therefore, when you crawl toward the edge of the turntable, you spin more slowly.
Chapter 8
Question 102
If the world’s populations moved to the North Pole and the South Pole, would the 24-hour day become longer, shorter, or stay the same?
Answer
It would become shorter.
Explanation
If the world’s populations moved to the poles, the mass of humans on Earth would become concentrated near Earth’s axis of rotation, which would cause the planet’s overall rotational inertia to decrease slightly. Since Earth’s angular momentum is constant, its rotational velocity would increase slightly (i.e., spin a little faster).
Chapter 8
Question 107
An automobile speedometer is configured to read speed proportional to the rotational speed of its wheels. If the oversize wheels of this red car were installed without making speedometer corrections, discuss whether the speedometer reading will be high or low—or no change.

Figure Q8.107
From Conceptual Physics (13th ed., p. 30) [Ebook], by P. G. Hewitt, 2021, Pearson. © 2021 by Pearson Education, Inc.
Answer
The reading will be low.
Explanation
The speedometer measures the rotational speed of the wheels and converts it into linear speed for the automobile. Using larger tires, the car will cover a greater distance for every rotation of its wheels. As a result, the speedometer will underestimate the actual speed of the car on the road.
Chapter 8
Question 109
In this chapter, you learned that an object may not be in mechanical equilibrium even when $\Sigma F = 0$. Discuss what else defines mechanical equilibrium.
Hint
How about $\Sigma \tau = 0$?
Diagram
Figure Q8.109
Answer
A possible situation is shown in Figure Q8.109, where two equal forces act in opposite directions on a disc. In this case, the net force on the disc is equal to zero. However, the disc experiences a nonzero net torque in the clockwise direction. As a result, the disc rotates about its center of mass without changing its location. Mechanical equilibrium is not achieved here because the second condition, $\Sigma \tau = 0$, is not satisfied.
Chapter 8
Question 117
Friction is needed for a car rounding a curve. But, if the road is banked, friction may not be required at all. What, then, supplies the needed centripetal force? (Hint: Consider vector components of the normal force on the car.)
Answer
The normal force.
Diagram
Figure Q8.117
Explanation
Assume slippery road conditions with almost no friction. The car in Figure Q8.117 is traveling away from you and turning left. In this case, only two forces are acting on the car: the downward force of gravity ($mg$) and the normal force ($N$) perpendicular to the surface of the road.
For the car to safely negotiate the curve, a horizontal centripetal force must act on the car to keep it on track. Note that the vertical force of gravity cannot contribute to the horizontal centripetal force. However, the normal force has a horizontal component ($N_x$) that provides the required centripetal force even in the absence of friction.
Exercises
Spend some time completing the following exercises to test your understanding of the main concepts in Chapter 8 and increase your efficiency in answering exam questions.
End-of-Chapter Practice Questions
Answer questions 1, 5, 11, 15, 21, 41, 43, 55, 57, 63, 69, 73, 75, 81, 85, 93, 101, and 111 in Chapter 8 of the eText. If you require assistance, please contact your tutor. The answers are provided at the end of the eText.