Unit 12: Solids
Did you know that both graphite and diamond are composed of pure carbon atoms? The differing properties of the two substances arise from their distinct crystal structures. After completing this unit, you should be able to describe the lattice structure of crystalline solids.
Learning Outcomes
By the end of this unit, you should be able to
- define the solid state of matter.
- explain the difference between crystalline and amorphous solids.
- describe the lattice structure of crystals.
- define density.
- explain the property of elasticity and the notions of tension and compression.
- explain why stone arches can stand for centuries.
eText Material
Reading Assignment
Read the following sections in Chapter 12 of the eText:
- 12.1: Crystal Structure
- 12.2: Density
- 12.3: Elasticity
- 12.4: Tension and Compression
- 12.5: Arches
- 12.6: Scaling
Supplementary learning resources are available on the Mastering Physics learning platform.
Additional Reading
Crystal Structure
An optical microscope consists of a system of lenses and uses visible light to produce magnified images of small objects like human tissue cells. However, such a device cannot be used to analyze the atomic structure of materials. This is because visible light has a wavelength in the range of 400–750 nanometers (nm), which is too large to resolve individual atoms.
The interatomic distances of most crystalline solids are in of the order of 0.1 nm. X‑rays, which have wavelengths appropriate for those distances, proved instrumental in mapping out the atomic structure of materials. When an X‑ray is applied to it, a crystal behaves like a diffraction grating, producing distinctive patterns of interference that can be recorded on film. Careful analysis of the diffraction pattern yields not only the spacing of atoms, but also the overall symmetry (cubic, hexagonal, etc.) of the crystal structure.
Elasticity
An external force applied on a body tends to deform it by changing its shape. However, a body with elastic properties (such as a spring) generates an opposing force, which restores the original shape once the external effects are removed.
Figure 12.1: A spring stretched by a force $F$.
Consider the spring in Figure 12.1, which has a normal length of $L_0$ when relaxed. If you pull the free end of the spring, it extends to the right to a new length $L$. Experimentally, you find that the applied force ($F$) is directly proportional to the change in length ($\Delta x = L - L_0$). This important property, referred to as Hooke’s law, is expressed mathematically as \begin{equation} F = k\, \Delta x \end{equation} The proportionality constant $k$ is called the spring constant, and it depends on the material and other physical properties of the spring.
Simulation
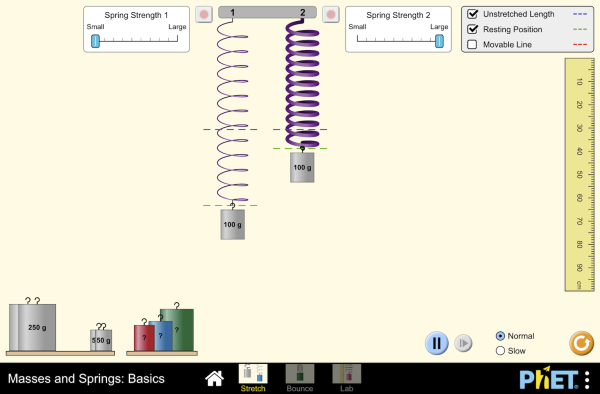
Run the Masses and Springs simulation, in which you hang masses from springs and discover how they stretch and oscillate.
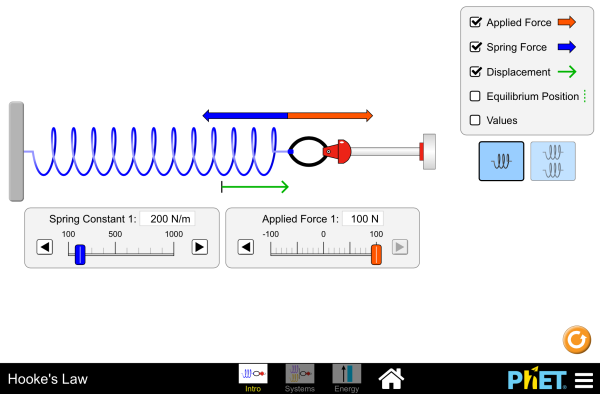
Run the Hooke’s Law simulation, in which you stretch and compress springs to explore the relationships between force, spring constant, and displacement.
Simulations by PhET Interactive Simulations, University of Colorado Boulder, licensed under CC-BY-4.0 (https://phet.colorado.edu)
Questions
The following questions are selected from the end of Chapter 12 of the eText. It is important to your learning that you try to answer each question independently before you read through the answer and explanation given.
For questions that ask you to explain, defend, or discuss your answer, the response revealed by the Answer button would earn you only partial marks on a quiz or exam in this course. Use the Answer to help you formulate a complete answer before you select the Explanation button to check your work.
Chapter 12
Question 30
Why can small creatures fall considerable distances without injury, while humans need parachutes to do the same?
Answer
Small creatures have more surface area per unit of body weight, so they experience greater air resistance per unit of body weight and therefore fall more slowly than humans.
Explanation
If you double the radius of a sphere, its volume (and weight) increases eight times, while its surface area become only four times larger. Therefore, the surface area per unit body of weight for a small creature, like an insect, is much greater than for a human. As a result, small creatures encounter greater air resistance than humans, resulting in a slower fall and softer impact with the ground.
An open parachute increases the effective surface area of a falling parachutist, which significantly increases the upward force of air resistance. Consequently, once the parachute is open, the parachutist experiences a slower descent toward the ground at a relatively low terminal speed.
Chapter 12
Question 39
A certain spring stretches 6 cm when a load of 30 N is suspended from it. How much will the spring stretch if 60 N is suspended from it (and it doesn’t reach its elastic limit)?
Answer
12 cm
Diagram
Figure Q12.39
Explanation
If a load of 30 N stretches the spring by 6 cm, the force required per unit of distance is expressed as \begin{equation} k = \frac{30\,\text{N}}{6\,\text{cm}} = 5\,\text{N}/\text{cm} \end{equation} where $k$ is the spring constant. In other words, the spring stretches by 1 cm for every 5 N of load. So a 60-N load would stretch the spring by \begin{align} \Delta x &= \frac{F}{k} \nonumber\\[6pt] & = \frac{60\,\text{N}}{5\,\text{N}/\text{cm}} \nonumber\\[6pt] &= 12\,\text{cm} \end{align} as shown in Figure Q12.39.
Chapter 12
Question 47
Your friend says that the primary difference between a solid and a liquid is the kind of atoms in the material. Do you agree or disagree, and why?
Answer
You disagree.
Explanation
Liquid water and ice, for example, are both made of H2O molecules. The difference between the two forms of water is in how the molecules are arranged and bonded. In solids, such as snow crystals, intermolecular attractive forces hold the molecules more tightly and arrange them in a regular pattern.
Chapter 12
Question 49
Silicon is the chief ingredient of both glass and semiconductor devices, yet the physical properties of glass are different from those of semiconductor devices. Explain.
Answer
In glass—an amorphous solid—the silicon atoms are distributed randomly in a noncrystalline (amorphous) structure. In semiconductor devices, the silicon atoms are arranged into a crystalline lattice to form a solid.
Chapter 12
Question 51
What happens to the density of air in a common rubber balloon when it is heated?
Answer
It decreases.
Explanation
When the balloon is heated, the air inside expands, thus increasing the volume of the balloon. Since no air is added or released, the same mass of air now occupies a larger volume. So the density of the air (mass per unit volume) has decreased.
Chapter 12
Question 53
What happens to the density of water when it freezes to become ice? Answer using a real-life example.
Hint
Note that an ice cube does not sink to the bottom of a glass of water.
Answer
It decreases. The density of water (at 4°C) is 1000 kg/m3, while the density of ice is 920 kg/m3. This means ice expands when it freezes, which can cause a glass bottle to explode when left in the freezer. This is also why ice cubes float on the surface of a glass of water.
Chapter 12
Question 71
Why is it easier to start a fire with kindling rather than with large sticks and logs of the same kind of wood?
Answer
Kindling wood receives more heat per unit mass.
Explanation
Kindling has more surface area per kilogram than logs and sticks, and most of the mass in small kindling is near the surface. Therefore, it is easier to heat kindling from all sides to the ignition temperature, creating flames that spread quickly. The heat supplied to a log, on the other hand, is not as concentrated, so the log takes longer to reach ignition temperature.
Chapter 12
Question 75
Some environmentally conscious people build their homes in the shape of a dome. Why is less heat lost in a dome-shaped dwelling than in a conventional dwelling with the same volume?
Answer
The dome has less surface area per unit volume.
Explanation
Since heat is lost through the outer walls of a building, the rate at which heat is lost is proportional to the surface area of the building. The external wall of a semispherical (dome-shaped) house has a smaller surface area than the external walls of a conventional block-shaped structure of the same volume.
Chapter 12
Question 78
Why do some animals curl up into a ball when they are cold?
Answer
To minimize heat loss.
Explanation
Out of all three-dimensional shapes, the ball (or sphere) has the smallest surface area per volume. Therefore, by curling up, animals minimize the rate at which heat leaves their bodies. Note that many animals, like penguins, huddle together to reduce the overall surface area exposed to extremely cold temperatures.
Chapter 12
Question 81
If you are grilling hamburgers and getting impatient, why is it a good idea to flatten the burgers to make them wider and thinner?
Answer
To increase the heat transfer per unit volume.
Explanation
By making the burger wider and thinner, you increase the surface area for the same volume of meat. As a result, more heat transfers from the barbecue grill to the meat, which causes the burger to cook faster.
Chapter 12
Question 95
If you use a batch of cake batter for cupcakes and bake them for the time suggested for baking a cake, what will be the result?
Answer
The cupcakes will overcook or even burn.
Explanation
Because of its smaller size, a cupcake has more surface area per volume than a regular cake. The oven heat thus reaches the inside of a cupcake sooner and at a higher rate per unit volume than it would for a regular size cake. Therefore, the baking time for a cake would be too long for the cupcakes.
Additional Questions
Answer the following additional questions (not found in your eText).
Unit 12
Question A
Determine the density of a 6-kg solid cylinder that is 10 cm tall and 10 cm in diameter.
Answer
7.6 g/cm3
Explanation
The volume of a cylinder of height $h = 10\,\text{cm}$ and radius $r = 5\,\text{cm}$ is calculated as follows: \begin{align} \text{Volume} &= \text{base area} \times \text{height} \nonumber\\[6pt] &= \pi r^2 \times h \nonumber\\[6pt] &= \pi\, (5\,\text{cm})^2 \times 10\,\text{cm} \nonumber\\[6pt] &= 785\,\text{cm}^3 \end{align} The cylinder has a mass of 6 kg (or 6000 g), so you calculate the density of the cylinder as follows: \begin{align} \text{Density} &= \frac{\text{mass}}{\text{volume}} \nonumber\\[6pt] &= \frac{6000\,\text{g}}{785\,\text{cm}^3} \nonumber\\[6pt] &= 7.6\,\text{g}/\text{cm}^3 \end{align}
Unit 12
Question B
In 2009, one of the U.S. government’s bailout packages was \$700 billion when gold was worth \$800 per ounce (\$28.40 per gram). Calculate the mass in grams of \$700 billion worth of gold. If this amount of gold were in the shape of a cube, how long would each of its sides be?[1]
Answer
$2.46\times 10^{10}\,\text{g}$, $10.8\,\text{m}$
Explanation
The mass of \$700 billion worth of gold is equal to \begin{align} \text{mass} &= \frac{700\times 10^9\,\text{dollar}}{28.40\,\text{dollar/g}} \nonumber\\[6pt] &= 2.46\times 10^{10}\,\text{g} \end{align} This is almost 25,000 metric tons, which is approximately 10 times the world’s gold production in 2009.
The volume of this huge amount of gold (density $= 19.3\,\text{g}/\text{cm}^3$) is calculated as follows: \begin{align} \text{Volume} &= \frac{\text{mass}}{\text{density}} \nonumber\\[6pt] &= \frac{2.46\times 10^{10}\,\text{g}}{19.3\,\text{g}/\text{cm}^3} \nonumber\\[6pt] &= 1.28\times 10^9\,\text{cm}^3 \nonumber\\[6pt] &= 1280\,\text{m}^3 \end{align} If this amount of gold were in the shape of a cube, then you calculate the length of one side by taking the cubic root of the volume: \begin{align} \text{Side length} &= \sqrt[3]{\text{volume}} \nonumber\\[6pt] &= \sqrt[3]{1280\,\text{m}^3} \nonumber\\[6pt] &= 10.8\,\text{m} \end{align}
Footnotes
[1] Hewitt, P. G. (2015). Conceptual Physics (12th ed., p. 241) [Ebook]. Pearson.
Exercises
Spend some time completing the following exercises to test your understanding of the main concepts in Chapter 12 and increase your efficiency in answering exam questions.
End-of-Chapter Practice Questions
Answer questions 5, 7, 13, 21, 25, 33, 37, 41, 43, 49, 55, 65, 73, 77, 79, 83, 91, 95, and 97 from Chapter 12 of the eText. If you require assistance, please contact your tutor. The answers are provided at the end of the eText.